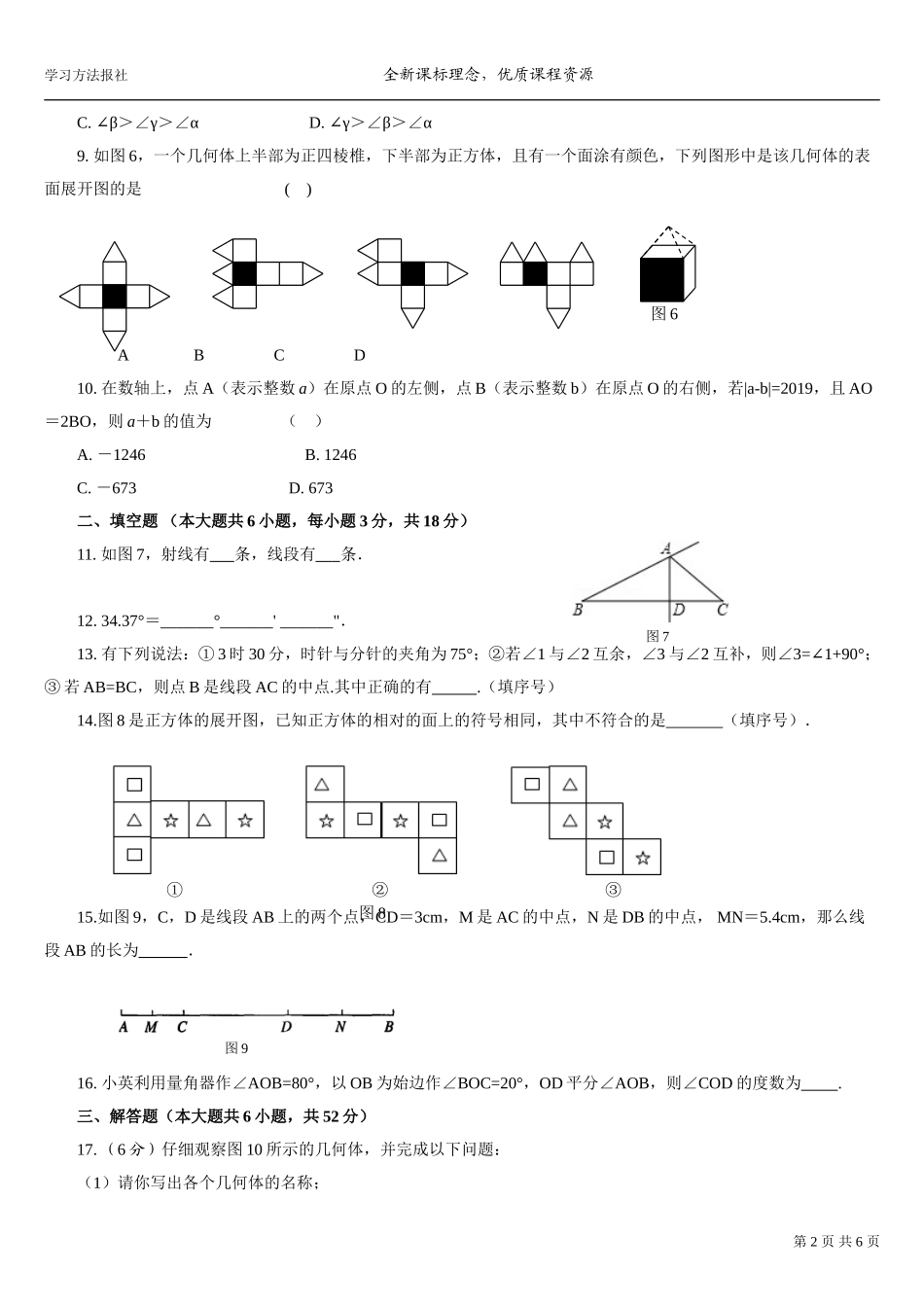
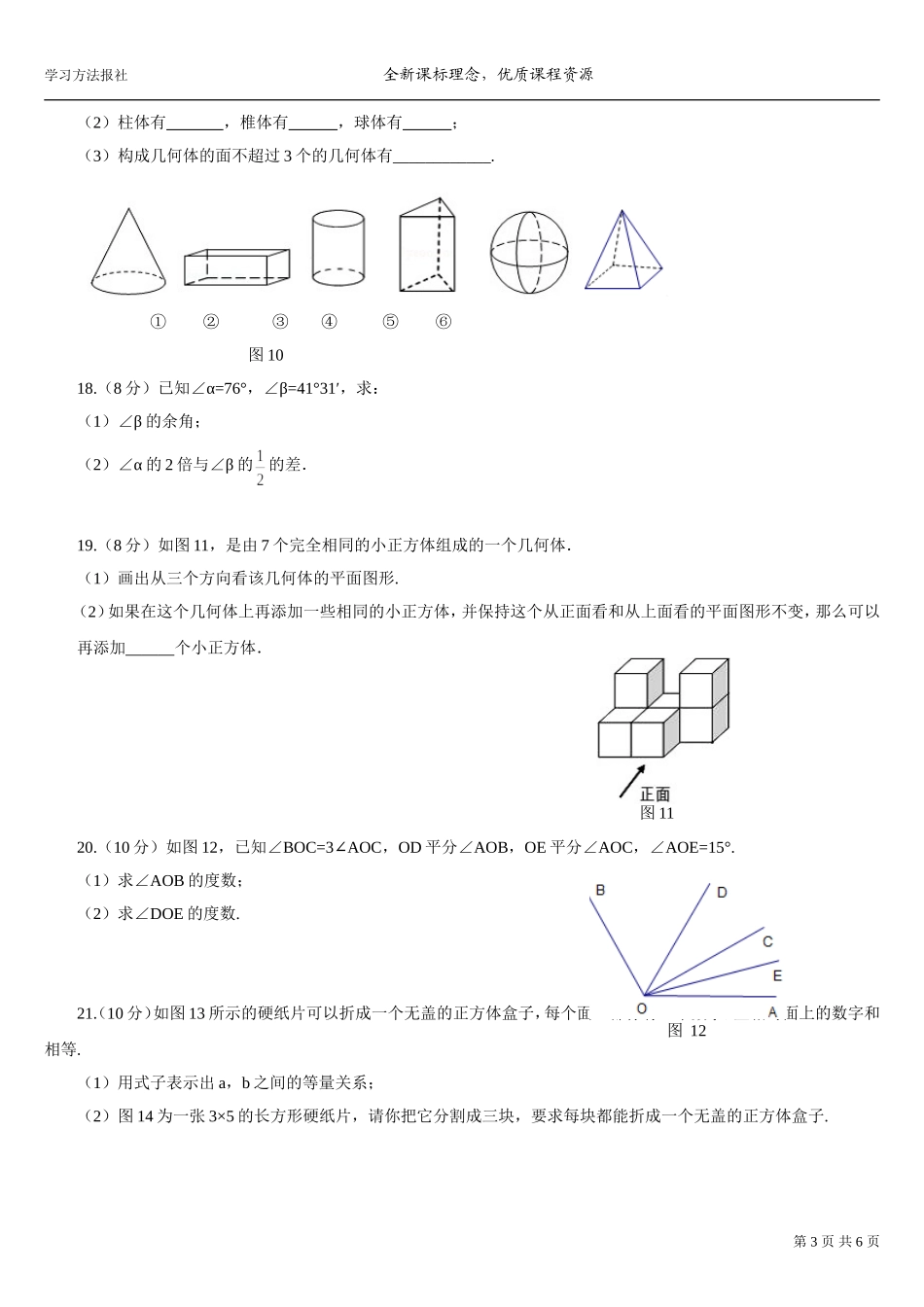
学习方法报社全新课标理念,优质课程资源第四章几何图形初步测试题(二)一、选择题(本大题共10小题,每小题3分,共30分)1.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是()A.三棱柱B.四棱柱C.三棱锥D.四棱锥2.由图1的五种基本图形中的两种拼接成图2,这两种基本图形是()A.①⑤B.②④C.③⑤D.②⑤3.已知一个角为55°,下列说法错误的是()A.这个角的余角为45°B.这个角的补角为125°C.这个角的补角比这个角的余角大90°D.这个角的一半为27.5°4.观察图4,有下列说法:①直线BA和直线AB是同一条直线;②射线AC和射线AD是同一条射线;③AB+BD>AD;④三条直线两两相交时,一定有三个交点.其中正确的有()A.1个B.2个C.3个D.4个5.从一个钝角的顶点,在它的内部引5条互不相同的射线,则该图中共有角的个数是()A.28B.21C.15D.66.如图4所示的立体图形,从正面看得到的平面图形是()7.如图5,已知OA表示北偏东30°方向,若射线OB与射线OA垂直,则OB表示的是()A.北偏西30°B.北偏西60°C.东偏北30°D.东偏北60°8.已知∠α=10°15′,∠β=610′,∠γ=10.2°,下列比较大小正确的是()A.α∠>∠β>∠γB.α∠>∠γ>∠β第1页共6页图1图2图3图4图5学习方法报社全新课标理念,优质课程资源C.β∠>∠γ>∠αD.γ∠>∠β>∠α9.如图6,一个几何体上半部为正四棱椎,下半部为正方体,且有一个面涂有颜色,下列图形中是该几何体的表面展开图的是()ABCD10.在数轴上,点A(表示整数a)在原点O的左侧,点B(表示整数b)在原点O的右侧,若|a-b|=2019,且AO=2BO,则a+b的值为()A.-1246B.1246C.-673D.673二、填空题(本大题共6小题,每小题3分,共18分)11.如图7,射线有条,线段有条.12.34.37°=°'".13.有下列说法:①3时30分,时针与分针的夹角为75°;②若∠1与∠2互余,∠3与∠2互补,则∠3=1+90°∠;③若AB=BC,则点B是线段AC的中点.其中正确的有.(填序号)14.图8是正方体的展开图,已知正方体的相对的面上的符号相同,其中不符合的是(填序号).15.如图9,C,D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长为.16.小英利用量角器作∠AOB=80°,以OB为始边作∠BOC=20°,OD平分∠AOB,则∠COD的度数为.三、解答题(本大题共6小题,共52分)17.(6分)仔细观察图10所示...