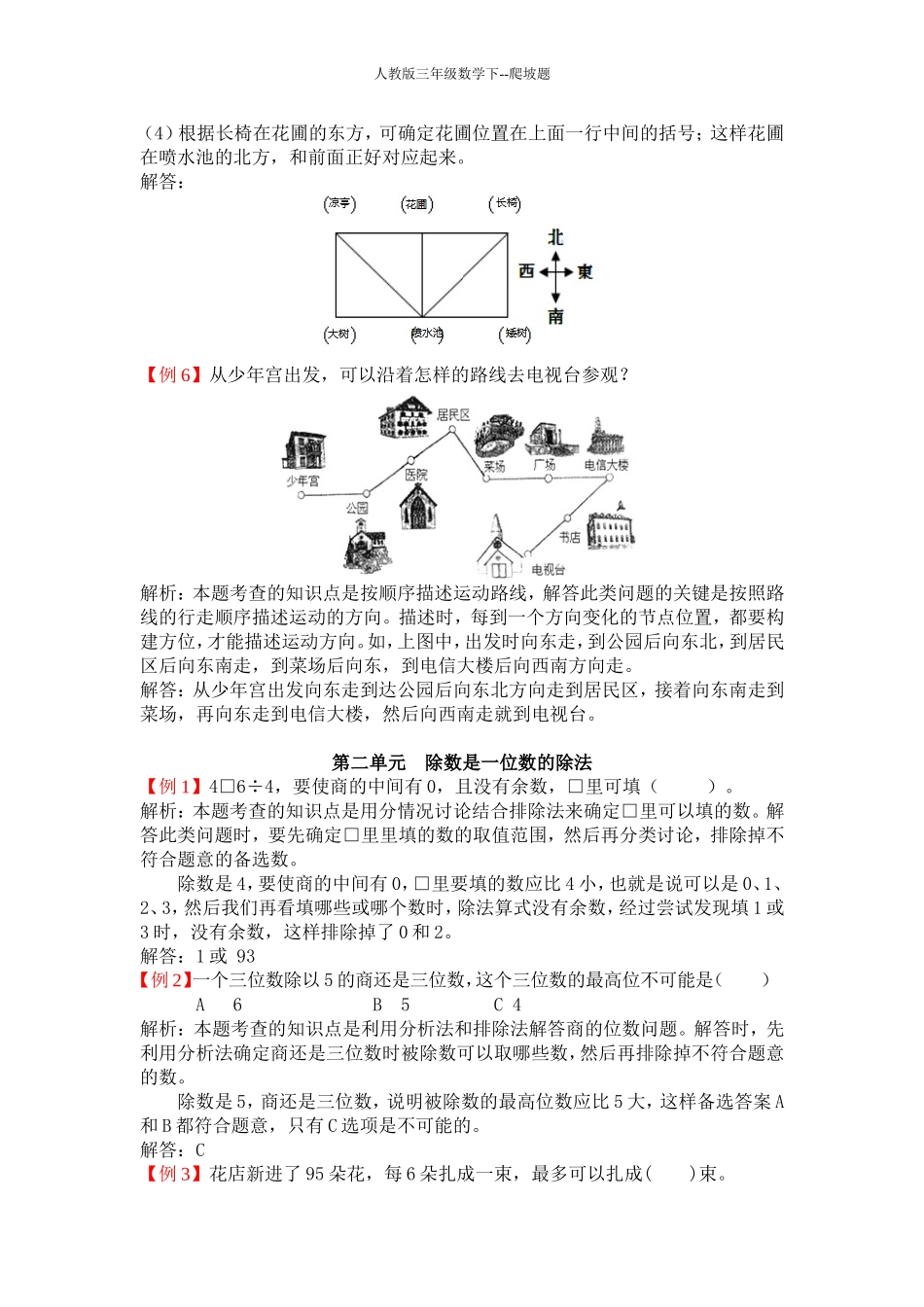
人教版三年级数学下--爬坡题第一单元位置与方向(一)【例1】早晨,面对太阳升起的方向,你的前面是()方,你的后面是()方,左面是()方,右面是()方。晚上,面向北极星的方向,你的后面是()方,左面是()方,右面是()方。解析:本题考查的知识点是根据已知条件用相对的方法确定方向,解答时抓住给出的可以判断已知方向的条件找到标准方向是解答此类问题的关键。早晨,面对太阳升起的方向,前面应是东方,和东相对的是西,所以后面是西这时左面应是北,右面是南。晚上,面向北极星的方向应是北方,这时后面应是和北相对的方向南方,左面应是西方,右面是东方。解答:东西北南南西东【例2】按要求画图形。(1)▲在▓的西南面;(2)◎在▓的东南面;(3)◆在▓的西北面;(4)●在▓的东北面。解析:本题考查的知识点是用对应法按要求画出图形指定的位置。解答时先找到给出的标准方向北,然后根据“上北下南、左西右东”来确定出“东北、西北、东南和西南”四个方向(如下图),最后再画出图形。解答:【例3】小强在小林的什么方向?小林在小强的什么方向?人教版三年级数学下--爬坡题解析:本题考查的知识点是根据不同的参照物确定物体的相对方向。解答时先找到给出的已知方向,然后再确定其它方向。站在小强位置看小林,小林在东北方向;站在小林位置看小强,小强在西南方向。解答:小强在小林的西南方向,小林在小强的东北方向。【例4】小红说:“我在小芳的南面.”小刚说:“我在小红的东北方向.”小丽说:“我在小刚的西北方向”.小明说:“我在小芳的西面”.他们的位置是()解析:本题考查的知识点是用推理分析的方法判断每个人的位置。解答时要根据每人的描述,以描述人为观察点来确定方向。先以小红为观察起点,小红在小芳的南方,以小红为观察点小刚在小红的东北方向;以小刚为观察点,小丽在小刚的西北方向;以小芳为观察点,小明在小芳的西面。(如下图)解答:A【例5】看下面的条件,然后在图中的括号内填上合适名称所对应的序号:(1)凉亭在喷水池的西北方;(2)大树在喷水池的西方;(3)矮树在长椅的南方;(4)喷水池在长椅的西南方;(5)长椅在花圃的东方;(6)花圃在喷水池的北方。解析:本题考查的知识点是根据图示方向标和方向的相对性来解答确定图形位置问题,解答此类问题常用的方法是综合分析法、对应法和推理法等。(1)根据凉亭在喷水池的西北方结合给出的西北方向的唯一性,可确定喷水池的位置是下...