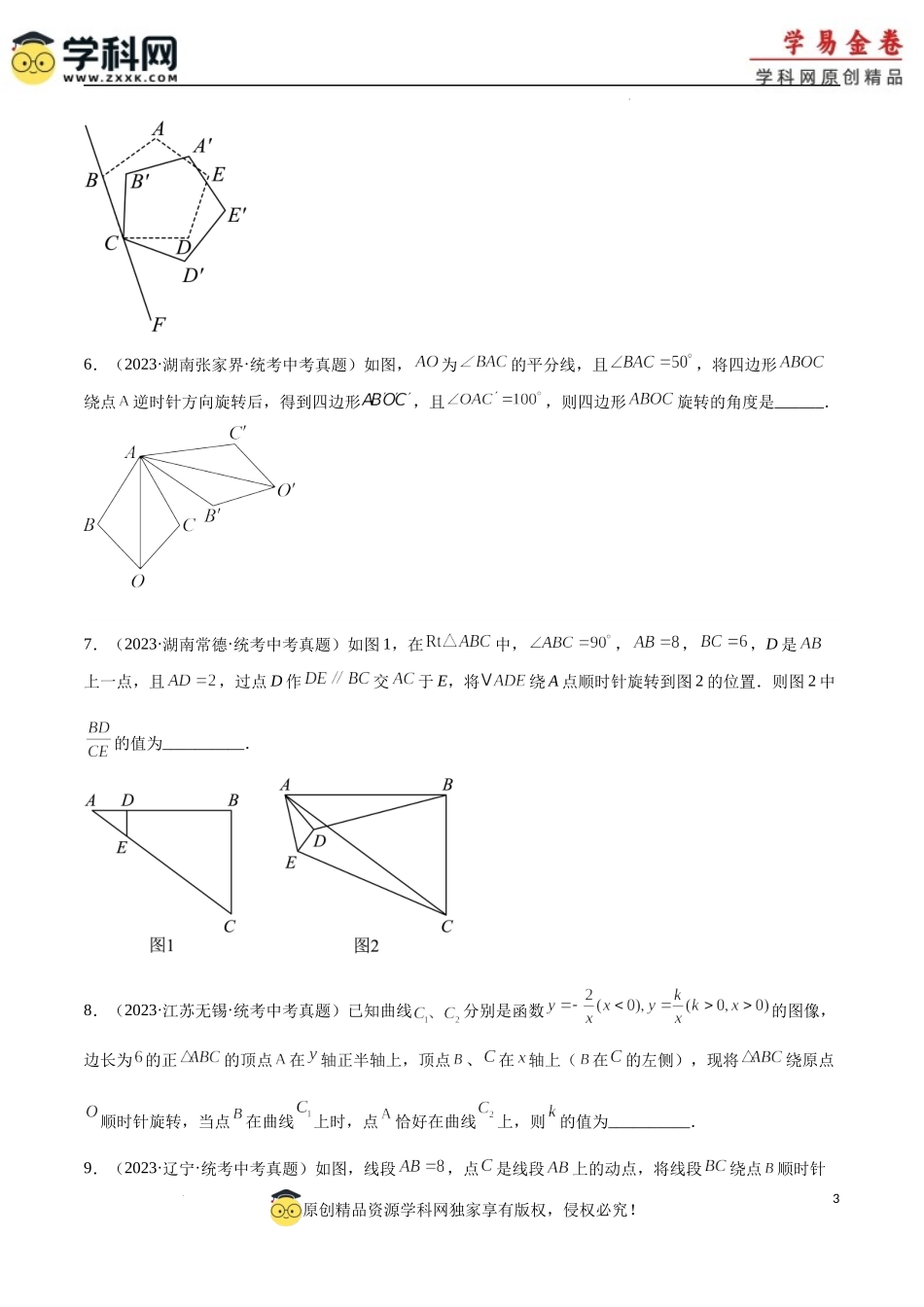
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司专题20图形的旋转(30题)一、单选题1.(2023·江苏无锡·统考中考真题)如图,中,,将逆时针旋转得到,交于F.当时,点D恰好落在上,此时等于()A.B.C.D.2.(2023·天津·统考中考真题)如图,把以点A为中心逆时针旋转得到,点B,C的对应点分别是点D,E,且点E在的延长线上,连接,则下列结论一定正确的是()A.B.C.D.3.(2023·四川宜宾·统考中考真题)如图,和是以点为直角顶点的等腰直角三角形,把以为中心顺时针旋转,点为射线、的交点.若,.以下结论:①;②;③当点在的延长线上时,;④在旋转过程中,当线段最短时,的面积为.其中正确结论有()2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司A.1个B.2个C.3个D.4个4.(2023·山东聊城·统考中考真题)如图,已知等腰直角,,,点C是矩形与的公共顶点,且,;点D是延长线上一点,且.连接,,在矩形绕点C按顺时针方向旋转一周的过程中,当线段达到最长和最短时,线段对应的长度分别为m和n,则的值为()A.2B.3C.D.二、填空题5.(2023·江苏连云港·统考中考真题)以正五边形的顶点C为旋转中心,按顺时针方向旋转,使得新五边形的顶点落在直线上,则正五边旋转的度数至少为______°.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司6.(2023·湖南张家界·统考中考真题)如图,为的平分线,且,将四边形绕点逆时针方向旋转后,得到四边形,且,则四边形旋转的角度是______.7.(2023·湖南常德·统考中考真题)如图1,在中,,,,D是上一点,且,过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为__________.8.(2023·江苏无锡·统考中考真题)已知曲线分别是函数的图像,边长为的正的顶点在轴正半轴上,顶点、在轴上(在的左侧),现将绕原点顺时针旋转,当点在曲线上时,点恰好在曲线上,则的值为__________.9.(2023·辽宁·统考中考真题)如图,线段,点是线段上的动点,将线段绕点顺时针4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司旋转得到线段,连接,在的上方作,使,点为的中点,连接,当最小时,的面积为___________.10.(2023·江西·统考中考真题)如图,在中,,将绕点逆时针旋转角()得到,连接,.当为直角三角形时,旋转角的度数为_______.11.(2023·上海·统考中...