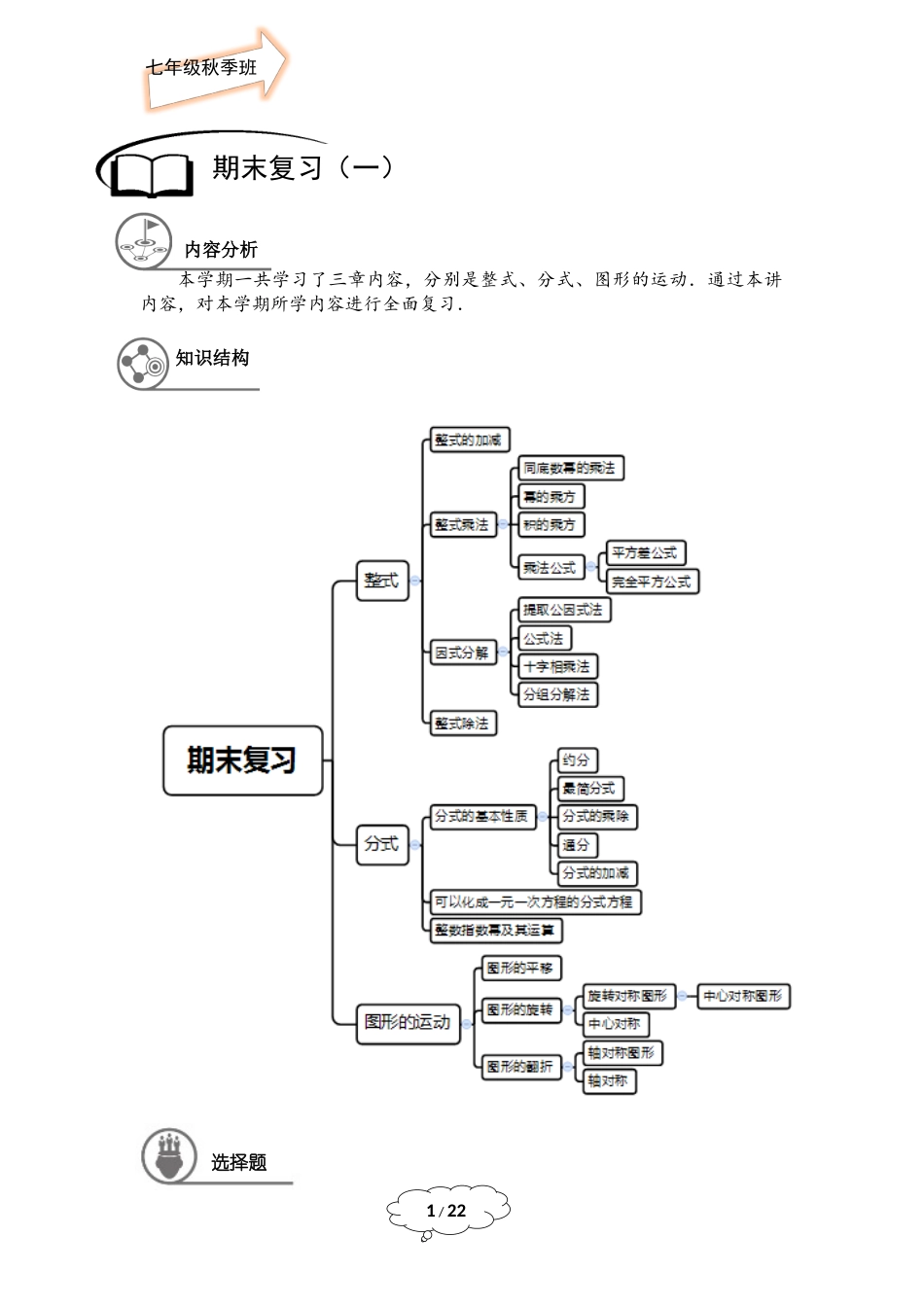
七年级秋季班1/22本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内容,对本学期所学内容进行全面复习.期末复习(一)内容分析知识结构选择题班秋季级年七2/22【练习1】下列各式中,与是同类项的是().....【难度】★【答案】B【解析】同类项是指(1)所含字母相同;(2)相同字母的指数相同.【总结】本题考查了同类项的定义.【练习2】如果分式有意义,那么应满足的条件是().....【难度】★【答案】B【解析】分式AB有意义指的是分母B≠0,即.【总结】本题考查了分式有意义的条件.【练习3】若,则等于().....【难度】★【答案】C【解析】x=(a+2b)2−(a−2b)2=8ab.【总结】本题考查了完全平方公式的公式变形.【练习4】下列图形中是旋转对称图形但不是中心对称图形的是().七年级秋季班3/22【难度】★【答案】A【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;旋转对称图形是指把一个图形绕一定点旋转一定角度(小于周角)后能与自身重合.【总结】本题考查了旋转对称图形和中心对称图形的概念.【练习5】下列等式中,从左到右的变形是因式分解的是().....【难度】★【答案】D【解析】因式分解是指把一个多项式化为几个整式的乘积的形式.【总结】本题考查了因式分解的概念.【练习6】的计算结果是()....【难度】★★【答案】C【解析】,同底数幂相除,底数不变,指数相减.【总结】本题考查了幂的乘方及同底数幂相除运算.【练习7】下列格式中,等式成立的是().....【难度】★★【答案】A【解析】A中x−yy−x=−(y−x)−(x−y)=y−xx−y正确.【总结】本题考查了分式的基本性质的运用.班秋季级年七4/22【练习8】如果将分式中的和都扩大到原来的倍,那么分式的值()..扩大到原来的倍.扩大到原来的倍.缩小到原来的.不变【难度】★★【答案】A【解析】和都扩大到原来的倍,即为3x和3y;则(3x)2−(3y)23x+3y=9x2−9y23x+3y=9(x2−y2)3(x+y)=3x2−y2x+y,所以原分式的值扩大到原来的3倍.【总结】本题考查了分式的基本性质的运用.【练习9】小敏和小明练习打字,小敏比小明每分钟多打个字,完成字文稿小敏比小明少用分钟,设小明每分钟打个字,则可列方程().....【难度】★★【答案】A【解析】解:设小明每分钟打x个字,则小敏每分钟打(x+25)个字,由题意得:,故选A.【总结】本题考查了列分式方程解应用题.【练习10】二次三项式分解因式的结果如...