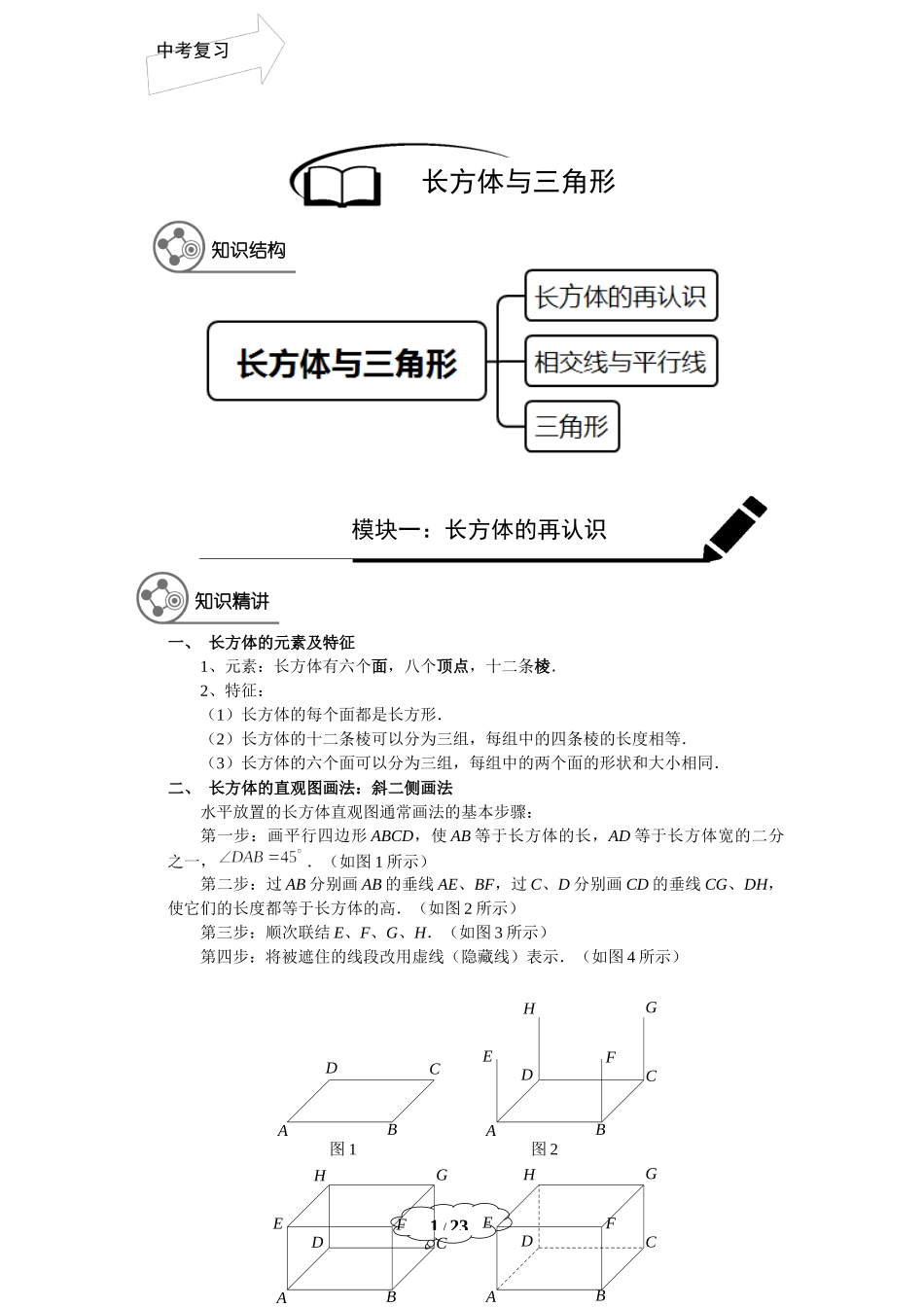
中考复习1/23一、长方体的元素及特征1、元素:长方体有六个面,八个顶点,十二条棱.2、特征:(1)长方体的每个面都是长方形.(2)长方体的十二条棱可以分为三组,每组中的四条棱的长度相等.(3)长方体的六个面可以分为三组,每组中的两个面的形状和大小相同.二、长方体的直观图画法:斜二侧画法水平放置的长方体直观图通常画法的基本步骤:第一步:画平行四边形ABCD,使AB等于长方体的长,AD等于长方体宽的二分之一,.(如图1所示)第二步:过AB分别画AB的垂线AE、BF,过C、D分别画CD的垂线CG、DH,使它们的长度都等于长方体的高.(如图2所示)第三步:顺次联结E、F、G、H.(如图3所示)第四步:将被遮住的线段改用虚线(隐藏线)表示.(如图4所示)长方体与三角形知识结构模块一:长方体的再认识图2图1HGFEDCBAHGFEDCBAHGFEDCBADCBA知识精讲习复考中2/23图4表示的长方体通常表示为ABCD-EFGH.它的六个面通常表示为:平面ABCD、平面ABFE、平面BCGF等.它的十二条棱通常分别表示为:棱AB、棱AE、棱EF等.三、长方体中棱与棱的位置关系如图4所示的长方体ABCD-EFGH中:棱EH与棱EF所在的直线在同一平面内,它们有唯一的公共点,我们称这两条棱相交.棱EF与棱AB所在的直线在同一平面内,但它们没有公共点,我们称这两条棱平行.棱EH与棱AB所在的直线既不平行,也不相交,我们称这两条棱异面.四、长方体中棱与平面的位置关系如图5,直线PQ垂直于平面ABCD,记作:直线PQ平面ABCD,读作:直线PQ垂直于平面ABCD.如图6,直线PQ平行于平面ABCD,记作:直线PQ//平面ABCD,读作:直线PQ平行于平面ABCD.如图4所示的长方体ABCD-EFGH中:棱EF与面BCGF,棱FG与面ABFE,棱BF与面ABCD都给我们以直线与平面垂直的形象.棱EF与面ABCD,棱BF与面ADHE,都给我们以直线与平面平行的形象.五、长方体中平面与平面的位置关系如图7,平面垂直于平面,记作平面平面,读作平面垂直于平面.如图8,平面平行于平面,记作平面//平面,读作平面平行于平面.如图4所示的长方体ABCD-EFGH中:面EFGH,面ABFE与面BCGF三个面中,任意两个都给我们以平面与平面垂直的形象.面ABCD与面EFGH,面BCGF与面ADHE,面ABFE与面DCGH,都给我们以平面与平面平行的形象.图6图5QPDCBAQPDCBA中考复习3/23【例1】如图,已知长方体ABCD-EFGH.(1)哪些棱与AB平行?(2)哪些棱与AB垂直?(3)哪些棱与AB异面?【难度】★【答案】(1)棱EF、HG、DC与AB平行;(2)棱EA、FB、DA、CB与AB相交...