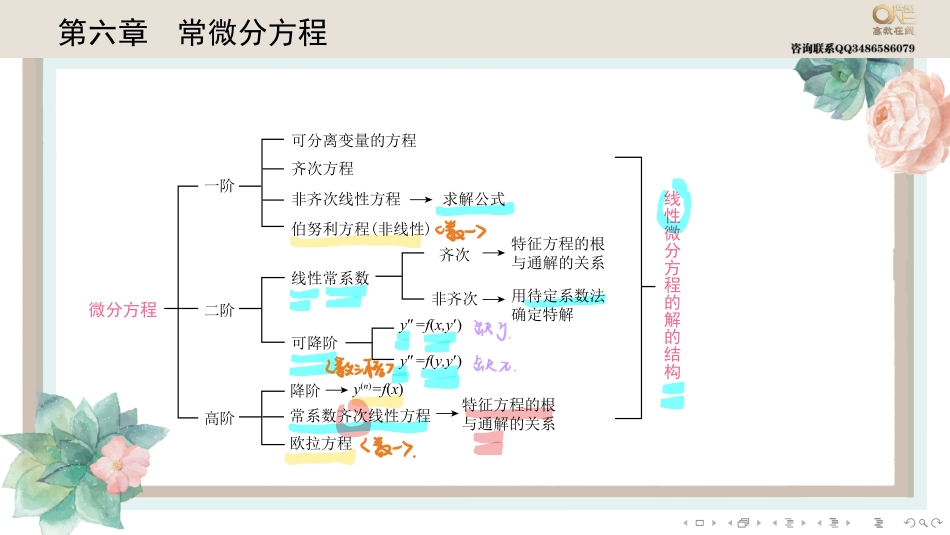
........第六章常微分方程�������������������������������������������������������������������������������y′=f(x,y′)′y′=f(y,y′)′�����������������������y(n)=f(x)���������������........第一节一阶微分方程微分方程的基本概念(1)微分方程一般地,凡表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程.(2)微分方程的阶微分方程中所出现的未知函数的最高阶导数的阶数,叫做微分方程的阶.(3)微分方程的解设方程F(x,y,y′,···,y(n))=0是n阶微分方程,函数y=φ(x)在区间I上有n阶连续导数.若在区间I上,F(x,φ(x),φ′(x),···,φ(n)(x))≡0,则函数y=φ(x)叫做微分方程F(x,y,y′,···,y(n))=0的解........(4)微分方程的通解与特解若微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数相同,则这样的解叫做微分方程的通解.确定了通解中的任意常数后,即得到微分方程的特解.(5)初值问题求微分方程y′=f(x,y)满足初始条件y|x=x0=y0的特解,这样的问题叫做一阶微分方程的初值问题.(6)积分曲线微分方程的解的图形是一条曲线,叫做微分方程的积分曲线.初值问题的几何意义,就是求微分方程的通过点(x0,y0)的那条积分曲线.二阶微分方程的初值问题{y′′=f(x,y,y′),y|x=x0=y0,y′|x=x0=y′0的几何意义,是求微分方程的通过点(x0,y0)且在该点处的切线斜率为y′0的那条积分曲线.........例1..已知y=xlnx是微分方程y′=yx+φ(xy)的解,则φ(xy)的表达式为()(A)−y2x2.(B)y2x2.(C)−x2y2.(D)x2y2........可分离变量的方程若一个一阶微分方程能写成g(y)dy=f(x)dx的形式,即能把微分方程写成一端只含y的函数和dy,一端只含x的函数和dx,则原方程称为可分离变量的微分方程.........例2..微分方程y′=y(1−x)x的通解是........齐次方程若一阶微分方程可化成dydx=φ(yx)的形式,则称该方程为齐次方程.齐次方程dydx=φ(yx)的解法作变换u=yx,则y=ux,dydx=xdudx+u.于是原方程可化为xdudx=φ(u)−u.用分离变量法求解后,代回u=yx并解出y即可.........例3..求xy′−y=√x2−y2满足y(1)=12的特解........一阶线性微分方程方程dydx+p(x)y=q(x)叫做一阶线性微分方程.若q(x)=0,则dydx+p(x)y=0是对应于dydx+p(x)y=q(x)的齐次线性方程.一阶非齐次线性微分方程的求解公式一阶非齐次线性微分方程y′+p(x)...