第3章 正弦交流电路(1).pdf

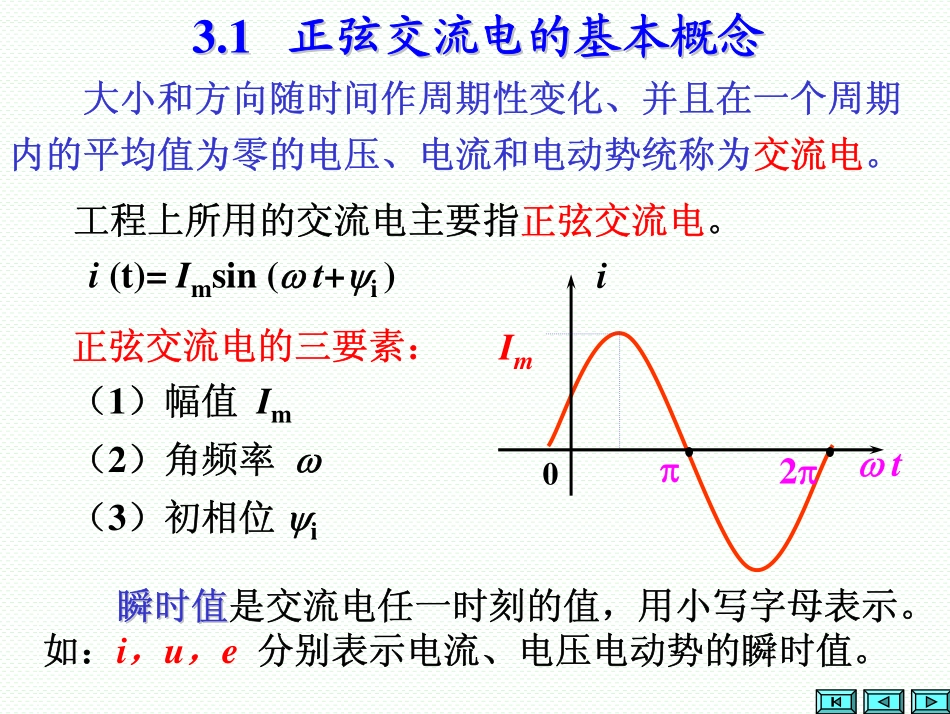
第第第第3 3 3 3章章章章 正弦交流电路正弦交流电路正弦交流电路正弦交流电路3.2 3.2 正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法3.3 3.3 单一参数的交流电路单一参数的交流电路单一参数的交流电路单一参数的交流电路3.4 3.4 正弦交流电路的分析正弦交流电路的分析正弦交流电路的分析正弦交流电路的分析3.6 3.6 交流电路的频率特性交流电路的频率特性交流电路的频率特性交流电路的频率特性3.5 3.5 正弦交流电路的功率正弦交流电路的功率正弦交流电路的功率正弦交流电路的功率3.7 3.7 电路中的谐振电路中的谐振电路中的谐振电路中的谐振3.1 3.1 正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念3.8 3.8 双口网络双口网络双口网络双口网络3.9 3.9 非正弦周期信号电路非正弦周期信号电路非正弦周期信号电路非正弦周期信号电路正弦交流电路是指含有正弦电源(激励)而且电路各部分正弦交流电路是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。所产生的电压和电流(响应)均按正弦规律变化的电路。第第第第3 3 3 3章章章章 正弦交流电路正弦交流电路正弦交流电路正弦交流电路在生产和生活中普遍应用正弦交流电，特别是三相电路在生产和生活中普遍应用正弦交流电，特别是三相电路应用更为广泛。应用更为广泛。本章将介绍交流电路的一些基本概念、基本理论和基本分析方法，为后面学习交流电机、电器及电子技术打下基础。本章将介绍交流电路的一些基本概念、基本理论和基本分析方法，为后面学习交流电机、电器及电子技术打下基础。本章还将讨论非正弦周期信号电路。本章还将讨论非正弦周期信号电路。交流电路具有用直流电路的概念无法理解和分析的物理交流电路具有用直流电路的概念无法理解和分析的物理现象，因此在学习时注意建立交流的概念，以免引起错误。现象，因此在学习时注意建立交流的概念，以免引起错误。大小和方向随时间作周期性变化、并且在一个周期大小和方向随时间作周期性变化、并且在一个周期内的平均值为零的电压、电流和电动势统称为内的平均值为零的电压、电流和电动势统称为交流电交流电。工程上所用的交流电主要指工程上所用的交流电主要指正弦交流电正弦交流电。i(t)=Imsin(t+i)正弦交流电的三要素：正弦交流电的三要素：（1）幅值）幅值 Im（2）角频率）角频率（3）初相位）初相位 i 3.1 3.1 正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念i0Im t2瞬时值瞬时值瞬时值瞬时值是交流电任一时刻的值，用小写字母表示。如：是交流电任一时刻的值，用小写字母表示。如：i，u，e 分别表示电流、电压电动势的瞬时值。分别表示电流、电压电动势的瞬时值。直流电路在稳定状态下电流、电压的大直流电路在稳定状态下电流、电压的大小和方向是不随时间变化的，如图小和方向是不随时间变化的，如图(a)所示。所示。tI U0正弦电压和电流是按正弦规律周期性正弦电压和电流是按正弦规律周期性变化的，其波形如图变化的，其波形如图(b)所示。所示。tu i0+uiR+uiR正半周正半周正半周正半周负半周负半周负半周负半周 电路图上所标的方向是指它们的参考电路图上所标的方向是指它们的参考方向，即代表正半周的方向。方向，即代表正半周的方向。负半周时，由于电压（或电流）为负值，负半周时，由于电压（或电流）为负值，所以其实际方向与参考方向相反。所以其实际方向与参考方向相反。+实际方向实际方向3.1 3.1 正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念图图(a)图图(b)最大值最大值初相位初相位角 频率角 频率i=Imsin(t+i)3.1 3.1 正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念=2 ff=T1Ti0tTT/2 t2 iIm3.1.1 正弦交流电的三要素正弦交流电的三要素1 1、最大值最大值最大值最大值最大值最大值最大值最大值是交流电的幅值，用大写字母加下标表示。是交流电的幅值，用大写字母加下标表示。如如Im、Um、Em。i0Im t23.1.1 正弦交流电的三要素正弦交流电的三要素3.1 3.1 正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念正弦交流电的基本概念T t2Im周期周期 T：正弦量变化一周所需要的时间；：正弦量变化一周所需要的时间；角频率 角频率 :例例3.1.1 我国和大多数国家的电力标准频率是我国和大多数国家的电力标准频率是50Hz，试求其，试求其周期和角频率。周期和角频率。解解=2 f=2 3.14 50=314rad/sTf1=S02.01=fTt0i频率频率 f：正弦量每秒内变化的次数；：正弦量每秒内变化的次数；fT22=Im交流电每交变一个周期便变化了交流电每交变一个周期便变化了2弧度，即弧度，即T=2 2、频率、周期、角频率、频率、周期、角频率 ti0 对于正弦量而言，所取计时起点不同，其初始值对于正弦量而言，所取计时起点不同，其初始值(t=0时的值时的值)就不同，到达幅值或某一特定值所需的时间也就不同。就不同，到达幅值或某一特定值所需的时间也就不同。i t0tIi sinm=00=i)sin(+=tIim sin0mIi=不等于零不等于零例如例如:t=0时，时，t=0时的相位角时的相位角 称为称为初相位角初相位角或或初相位。初相位。(t+)称为正弦量的称为正弦量的相位角相位角或或相位。相位。它反映出正弦量变化的进程。它反映出正弦量变化的进程。若所取计时起点不同，则正弦量若所取计时起点不同，则正弦量初相位不同。初相位不同。i03 3、初相位初相位初相位初相位有效值有效值有效值有效值是从电流的热效应来规是从电流的热效应来规是从电流的热效应来规是从电流的热效应来规定的定的定的定的。如果如果如果交流电流通过一个电阻时在一个周期内消耗的电能与某直流电流通过同一电阻在相同时间内消耗的电能相等如果交流电流通过一个电阻时在一个周期内消耗的电能与某直流电流通过同一电阻在相同时间内消耗的电能相等,就将这一直流电流的数值定义为交流电流的有效值。就将这一直流电流的数值定义为交流电流的有效值。)sin(im +=tIi=TtiTI02d12mII=2mUU=t2Imt0iIm同理可得同理可得根据上述定义，有根据上述定义，有有效值有效值当电流为正弦量时当电流为正弦量时:2mEE=Ri2dt=RI2T0T3.1.2 有效值有效值有效值有效值有效值用大写字母表示。如有效值用大写字母表示。如 I、U、E。0 tiu=Umsin(t+1)ui=Imsin(t+2)当两个同频率的正弦量计时起点改变时，它们的初相位改变，但相位差不变。当两个同频率的正弦量计时起点改变时，它们的初相位改变，但相位差不变。两个同频率正弦量的相位角两个同频率正弦量的相位角之差称为之差称为相位差相位差，用，用 表示。表示。=(t+1)(t+2)=1 2iu 2 1 图中图中 1 2即即u 比比i 超前超前 角角或称或称 i 比比 u 滞后滞后 角角 ti0i1i2i3i1与与i3反相反相i1与与i2同相同相3.1.3 相位差相位差正弦电量（时间函数）正弦量运算所求正弦量正弦电量（时间函数）正弦量运算所求正弦量变换变换相量（复数）相量结果相量（复数）相量结果反变换反变换相量运算（复数运算相量运算（复数运算)正弦量具有幅值、频率和初相位三个要素，它们除了用三角正弦量具有幅值、频率和初相位三个要素，它们除了用三角函数式和正弦波形表示外，还可用函数式和正弦波形表示外，还可用相量相量来表示同频率的正弦量。来表示同频率的正弦量。正弦量的正弦量的相量表示法相量表示法就是用就是用复数复数来表示正弦量。来表示正弦量。相量法相量法是一种用来表示和计算同频率正弦量的数学工具，是一种用来表示和计算同频率正弦量的数学工具，应用相量法可以使正弦量的计算变得很简单。应用相量法可以使正弦量的计算变得很简单。例如，已知两个支路电流例如，已知两个支路电流i1=I1 msin(t+i1)i2=I2 msin(t+i2)若需求：若需求：i1+i23.2 3.2 正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法+1+j0例如：例如：t=t1时，时，i(t1)=Imsin(t1+)t1+Im ti 0 t1 A t2+Ai=Imsin(t+)有向线段长度是有向线段长度是Im，t=0时，与横轴的夹角是时，与横轴的夹角是，以角速度以角速度 逆时针方向旋转，它在逆时针方向旋转，它在虚轴上的投影，虚轴上的投影，即为正弦电流的即为正弦电流的瞬时值。瞬时值。正弦量可用旋转有向线段表示正弦量可用旋转有向线段表示3.2 3.2 正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法aA0 b+1+jr模模幅角幅角a=rcos b=rsin r=a2+b2=arctanbacos+jsin=ej 由欧拉公式，得出：由欧拉公式，得出：A=a+jb=r(cos+jsin)=rej=r 三角式三角式代数式代数式指数式指数式极坐标式极坐标式复数在进行加减运算时应采用代数式，复数在进行加减运算时应采用代数式，实部与实部相加减，虚部与虚部相加减。实部与实部相加减，虚部与虚部相加减。复数在进行乘运算时应采用指数式或极坐标式，模与模相乘，幅角与幅角相加。复数在进行乘运算时应采用指数式或极坐标式，模与模相乘，幅角与幅角相加。有向线段可用复数表示有向线段可用复数表示复数复数可用几种形式表示可用几种形式表示1j=复数在进行除运算时应采用指数式或极坐标式，模与模相除，幅角与幅角相减。复数在进行除运算时应采用指数式或极坐标式，模与模相除，幅角与幅角相减。由以上分析可知，一个复数由模和幅角两个特征量确定。由以上分析可知，一个复数由模和幅角两个特征量确定。而正弦量具有幅值、初相位和频率三个要素。但在分析线性电而正弦量具有幅值、初相位和频率三个要素。但在分析线性电路时，电路中各部分电压和电流都是与电源同频率的正弦量，路时，电路中各部分电压和电流都是与电源同频率的正弦量，因此，频率是已知的，可不必考虑。故一个正弦量可以由幅值因此，频率是已知的，可不必考虑。故一个正弦量可以由幅值和初相位两个特征量来确定。和初相位两个特征量来确定。比照复数和正弦量，正弦量可用复数来表示其幅值和初相位两个要素。复数的模即为正弦量的幅值或有效值，复数的幅角即为正弦量的初相位。比照复数和正弦量，正弦量可用复数来表示其幅值和初相位两个要素。复数的模即为正弦量的幅值或有效值，复数的幅角即为正弦量的初相位。为与复数相区别，把表示正弦量的复数称为相量。并在大为与复数相区别，把表示正弦量的复数称为相量。并在大写字母上打一写字母上打一“”。I=I =Iej=I(cos+jsin)(有效值相量有效值相量)Im=Im =Imej=Im(cos+jsin)(最大值相量最大值相量)sin(+=tIim的相量式为例如的相量式为例如=Ia+j Ib=Icos+jIsin=Iej=I 最大值相量最大值相量有效值相量有效值相量0Im+1+jI IaIbI=Ia m+j Ibm=Imcos+jImsin=Imej=Im Im相量图相量图相量是相量是表示表示表示表示正弦交流电的复数，正弦交流正弦交流电的复数，正弦交流电是时间的函数，所以二者之间并电是时间的函数，所以二者之间并不不不不相等相等相等。相等。正弦量正弦量用旋转有向线段表示用旋转有向线段表示用复数表示，同频率正弦量用复数表示，同频率正弦量可以用可以用复数复数来表示，称之为来表示，称之为相量相量。用大写字母上打。用大写字母上打“”表示。表示。IUmi=Imsin(t+)相量是相量是表示表示表示正弦交流电的复数，正弦交流电是表示正弦交流电的复数，正弦交流电是时间的函数，二者之间并时间的函数，二者之间并不相等不相等不相等。不相等。按照正弦量的大小和相位关系画出的若干个相量的图形，按照正弦量的大小和相位关系画出的若干个相量的图形，称为称为相量图相量图。注意注意只有正弦量才能用相量表示；只有正弦量才能用相量表示；只有同频率的正弦量才能画在同一相量图上；只有同频率的正弦量才能画在同一相量图上；相量图相量图1j0 i1 i2I1mI2m例例 若若 i1=I1 msin(t+i1)i2=I2 msin(t+i2)，画相量图。画相量图。设设i1=30，i2=65。例例3.2.1 若已知若已知 i1=I1 msin(t+i1)、i2=I2 msin(t+i2)，求求 i1+i2解：用相量图求解解：用相量图求解1j0 i1 i2ImIm1Im2 ii=Imsin(t+i)3.2 3.2 正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法正弦交流电的相量表示法例例3.2.2 若已知若已知 i1=I1msin(t+1)=100sin(t+45)A，i2=I2msin(t+2)=60sin(t 30)A，试求，试求 i=i1+i2。解解:+=+=+=+=j30-j452m1mme60e100III?Ae129)03j52()7.70j7.70(02j18 =+=+=A)0218sin(129+=+=ti 于是得于是得正弦电量的运算可按正弦电量的运算可按下列步骤下列步骤进行进行正弦电量（时间函数）正弦量运算所求正弦量正弦电量（时间函数）正弦量运算所求正弦量变换变换相量（复数）相量结果相量（复数）相量结果反变换反变换相量运算（复数运算相量运算（复数运算)例例3.2.3 已知某正弦电压已知某正弦电压Um=311V，f=50Hz，u=30，试写出此电压的最大值相量、有效值相量和瞬时值表达式画出此电压的相量图，求，试写出此电压的最大值相量、有效值相量和瞬时值表达式画出此电压的相量图，求t=0.01S时电压的瞬 时值。时电压的瞬 时值。解：解：瞬时值瞬时值u=311sin(100 t+30)=311 30 VUmu(0.01)=311sin(100 0.01+30)=155.5VU30=220VU=2Um=2311=220 30 VU有效值相量有效值有效值相量有效值最大值相量最大值相量电路分析是确定电路中电路分析是确定电路中电路分析是确定电路中电路分析是确定电路中电压与电流电压与电流电压与电流电压与电流关系及关系及关系及关系及能量的转换能量的转换能量的转换能量的转换问题。问题。问题。问题。3.3.1 3.3.1 电阻元件电阻元件电阻元件电阻元件的交流电路的交流电路的交流电路的交流电路iRu=本节从电阻、电感、电容两端电压与电流一般关系式入本节从电阻、电感、电容两端电压与电流一般关系式入本节从电阻、电感、电容两端电压与电流一般关系式入本节从电阻、电感、电容两端电压与电流一般关系式入手，介绍在正弦交流电路中这些手，介绍在正弦交流电路中这些手，介绍在正弦交流电路中这些手，介绍在正弦交流电路中这些理想元件的理想元件的理想元件的理想元件的电压电压电压电压与与与与电流电流电流电流之间之间之间之间的的的的关系及关系及关系及关系及能量转换能量转换能量转换能量转换问题。为问题。为问题。为问题。为分析分析分析分析交流电路交流电路交流电路交流电路奠定奠定奠定奠定基础。基础。基础。基础。R+ui1.电压与电流的关系电压与电流的关系在电阻元件的交流电路中，电压、电流参考方向如图所示。根据欧姆定律设在电阻元件的交流电路中，电压、电流参考方向如图所示。根据欧姆定律设tIim sin=tUtRIRium sinsinm=则则mm式中式中RIU=或或RIUIU=mm可见，可见，R 等于电压与电流有效值或最大值之比。等于电压与电流有效值或最大值之比。3.3 3.3 单一参数的交流电路单一参数的交流电路单一参数的交流电路单一参数的交流电路电压与电流同频率、同相位；电压与电流同频率、同相位；1.1.电压电压电压电压与与与与电流电流电流电流的的的的关系关系关系关系电压与电流大小关系电压与电流大小关系iu波形图波形图UI电压与电流相量表达式电压与电流相量表达式 t0相量图相量图+1+j03.3.1 3.3.1 电阻元件的交流电路电阻元件的交流电路电阻元件的交流电路电阻元件的交流电路tUtRIRium sinsinm=RIU=UR I=R+uitIim sin=U=UuI=Ii瞬时功率瞬时功率平均功率平均功率2.2.功率功率功率功率u t0ip0 tP=U I转换成的热能转换成的热能tIim sin=tUu sinm=)2cos1(tUIuip =PtW=R+uiRIRUUItpTPT220d1=设设0fXL感抗感抗1.1.电压电压电压电压与与与与电流电流电流电流的的的的关系关系关系关系由，由，有有感抗与频率感抗与频率 f 和和L成正比。因此，电成正比。因此，电感线 圈对高 频电流的阻碍作用很大，而感线 圈对高 频电流的阻碍作用很大，而对直流可视为短路。对直流可视为短路。3.3.2 3.3.2 电感元件的交流电路电感元件的交流电路电感元件的交流电路电感元件的交流电路tIim sin=tiLudd=)90sin(cosmm+=+=tUtILuLmmmXILIU=式中式中LXL=fLXL2=设在电感元件的交流电路中，电压、电流取关联参考方向。设在电感元件的交流电路中，电压、电流取关联参考方向。+uiLXL与与 f 的关系的关系（1 1）u u 和和和和 i i 的频率相同；的频率相同；的频率相同；的频率相同；（2 2）u u 在相位上超前于在相位上超前于在相位上超前于在相位上超前于 i i 90 ；（3 3）u u 和和和和 i i 的最大值和有效值之间的关系为：的最大值和有效值之间的关系为：的最大值和有效值之间的关系为：的最大值和有效值之间的关系为：Um=XLImU=XLI用相量法可以把电感的电压和电流的上面三方面用相量法可以把电感的电压和电流的上面三方面的关系的的关系的(2)和和(3)统一用相量表示：统一用相量表示：Um=j XLImU=j XLI即即:j I=I ej90=I e j iiej90=Iej(+90)iiii因因jiiI 相当于将相量相当于将相量 I 逆时针转了逆时针转了90 iiiiU+1+j0I相量图相量图由上面的分析可知电感的电压和电流的关系为由上面的分析可知电感的电压和电流的关系为ui波形图波形图 t0U+1+j01.1.电压电压电压电压与与与与电流电流电流电流的的的的关系关系关系关系电压超前电流电压超前电流90；相量图电压与电流大小关系相量图电压与电流大小关系电压与电流相量式电压与电流相量式tsinm Ii=)90sin(m+=+=tUu LIXU=jILUX=+uiL3.3.2 3.3.2 电感元件的交流电路电感元件的交流电路电感元件的交流电路电感元件的交流电路I波形图波形图2.功率功率iu+Lp=u i=UI sin2 t瞬时功率瞬时功率i=Imsin tu=Umsin(t+90)iu t0p t0+当当u、i同号时（同号时（i增大）增大）p0,电感吸收功率；电感吸收功率；当当u、i异号时（异号时（i减小）减小）p0,电感吸收功率；当电感吸收功率；当u、i实际方向相反时（实际方向相反时（i 减小）减小）p0,电容吸收功率；电容吸收功率；当当u、i异号时（异号时（u减小）减小）p0,电容吸收功率；当电容吸收功率；当u、i实际方向相反时（实际方向相反时（u减小）减小）p XC 时时,X 0，为正，电路中电压超前电流，电路呈电感性；为正，电路中电压超前电流，电路呈电感性；当当XL XC 时时,X 0，网络吸收电功率，网络吸收电功率当当u、i 异号时，异号时，p 0的面积大于的面积大于p 0 的面积。表明平均功率不为的面积。表明平均功率不为0。网络内部有电阻（耗能）元件。网络内部有电阻（耗能）元件。)2cos(cos +=tUIUIp瞬时功率瞬时功率uip tu i pu+iuN03.5.1 瞬时功率瞬时功率)2cos(cos +=tUIUIp+=+=TTttUIUITtpTP00d)2cos(cos1d1 cosUI=瞬时功率瞬时功率有功功率有功功率（平均功率）为（平均功率）为2IZUIS=无功功率无功功率为为电压与电流的有效值之积，称为电路的电压与电流的有效值之积，称为电路的视在功率视在功率单位是单位是(VA)或或(kV A)3.5.2 有功功率、无功功率和视在功率有功功率、无功功率和视在功率Q=UIsin 功率因数功率因数=cos u=Usin(t+)2i=I sin t2uip tu i pp=u.i=UIcos-UIcos(2 t+)有功功率有功功率=UIcos T10Tu i dtP=P 无功功率无功功率Q=UIsin 瞬时功率瞬时功率视在功率视在功率S=UI 3.5.2 有功功率、无功功率和视在功率有功功率、无功功率和视在功率有功功率、无功功率和视在功率有功功率、无功功率和视在功率功率三角形功率三角形有功功率有功功率P=UIcos 无功功率无功功率 Q=U I sin 视在功率视在功率S=UIS2=P2+Q2S=P2+Q2SPUURUXRXZQ 1、阻抗三角形、阻抗三角形2、电压三角形、电压三角形3、功率三角形3、功率三角形u=Usin(t+)2i=I sin t2解解:例例3.5.1 R、L、C串联交流电路如图所示。已知串联交流电路如图所示。已知R=30、L=127mH、C=40 F，。求：，。求：(1)电流电流 i 及各部分电压及各部分电压uR，uL，uC;(2)求功率求功率P 和和Q。V)20314sin(2220o+=+=tu+L+uCRiuLuCuR+=40101273143LXL=801040314116CXC 80)-40(j30)j(+=+=CLXXRZ=5350)40j30(20220VU=20220734.4A5350UIZ=?A)73314sin(24.4+=+=ti(1)于是得于是得A73132734.430=IRUR?V)73314sin(2132+=+=tuRV163176734.4j40j=IXULL?V)163314sin(2176+=+=tuLV17352734.480jj=IXUCC?V)17314sin(2352=tuCCLRUUUU?+=CLRUUUU+)53cos(4.4220cos=UIPW8.5806.04.4220=)53sin(4.4220sin=UIQvar4.774)8.0(4.4220=注意：注意：（2）电路为电容性电路为电容性例例3.5.2 试求电路中的有功功率试求电路中的有功功率P,无功功率无功功率Q，视在功率，视在功率S 及功率因数及功率因数cos，已知：，已知：=100 0V。UIj4 3 +UI1I2 j2 解：方法一解：方法一Z=(3+j4)(j2)3+j4j26j+83+j2=10 36.873.6 33.69=2.78 70.56 I=UZ=100 02.78 70.56=36 70.56 AP=UIcos=10036cos(70.56)=1200WQ=UIsin=10036sin(70.56)=3400varS=UI=100 36=3600V Acos=cos(70.56)=0.33 解：方法 二解：方法 二I1=U|Z1|=1005=20AI2=U|Z2|1002=P=I12R=2023=1200WQC=I22XC=5022=5000varQ=QL+QC=16005000=3400var=arctgQ/P=70.56cos=cos(70.56)=0.33 S=50AQL=I12XL=2024=1600varP2+Q2=3600VA例例3.5.2 试求电路中的有功功率试求电路中的有功功率P,无功功率无功功率Q，视在功率，视在功率S 及功率因数及功率因数cos，已知：，已知：=100 0V。UIj4 3 +UI1I2 j2 功率因数低引起的问题功率因数低引起的问题有功功率有功功率P=UNINcos 功率因数功率因数P=UI cos (1)电源设备的容量不能充分利用(1)电源设备的容量不能充分利用(2)增加输电线路和发电机绕组的功率损耗(2)增加输电线路和发电机绕组的功率损耗在在P、U一定的情况下，一定的情况下，cos 越低，越低，I 越大，损耗越大。越大，损耗越大。情况下，情况下，cos 越低，越低，P越小，设备得不到充分利用。越小，设备得不到充分利用。电压与电流的相位差电压与电流的相位差(功率因数角功率因数角)在电源设备在电源设备UN、IN一定的一定的 2222cos1)(UPrrIP=3.5.3 功率因数的提高功率因数的提高1、提高功率因数的意义提高功率因数的意义提高功率因数的方法提高功率因数的方法+uiiRLLRCiCIICIRLU 1 电路功率因数低的原因电路功率因数低的原因并联电容后，电感性负载的工作并联电容后，电感性负载的工作状态没变，但电源电压与电路中总电状态没变，但电源电压与电路中总电流的相位差角减小，即提高了整个电流的相位差角减小，即提高了整个电路的功率因数。路的功率因数。通常是由于存在电感性负载通常是由于存在电感性负载将适当的电容与电感性负载并联将适当的电容与电感性负载并联因因 cos 12、提高功率因数的方法提高功率因数的方法提高功率因数的方法提高功率因数的方法+uiiRLLRCiCIICIRLU 1 Ucos I=PUcos 1IRL=PP=UIRLcos 1=UIcos IC=IRLsin 1 Isin Psin Ucos 1IC=Psin 1Ucos U P(tan 1 tan)=C=U 2P(tan 1 tan)IC=UXC=U C已知感性负载的功率及功率因数已知感性负载的功率及功率因数cos 1，若要求把电路功率因数提高到，若要求把电路功率因数提高到cos，则应并联电容，则应并联电容C 为为F656)18tan53(tan220502101023=C=536.0cos11=1895.0cos例例3.5.3 有一电感性负载，有一电感性负载，P=10kW，功率因数，功率因数cos 1=0.6，接在电压，接在电压U=220V的电源上，电源频率的电源上，电源频率f=50Hz。(1)如果将功率因数提高到如果将功率因数提高到cos=0.95，试求与负载并联的电容器的电容值和电容并联前后的线路电流。，试求与负载并联的电容器的电容值和电容并联前后的线路电流。(2)如果 将功 率 因数从如果 将功 率 因数从0.95再提高到再提高到1，试问并联电容器的电容值还需增加多少？，试问并联电容器的电容值还需增加多少？解解:所需电容值为所需电容值为电容并联前线路电流为电容并联前线路电流为A6.75A6.02201010cos311=UPI电容并联后线路电流为电容并联后线路电流为A8.47A95.02201010cos3=UPIF6.213)0tan18(tan220502101023=C（2）若 将功 率 因数从）若 将功 率 因数从0.95再提高到再提高到1，所需并联电容值为（，所需并联电容值为（1）C=U 2P(tan 1 tan)例例3.5.4 某小水电站有一台额定容量为某小水电站有一台额定容量为10kVA的发电机，的发电机，额定电压为额定电压为220V，额定频率，额定频率f=50Hz，今接一感性负载，今接一感性负载,其功率为其功率为8kW，功率因数，功率因数cos 1=0.6，试问：，试问：1.发电机的电流是否超过额定值？发电机的电流是否超过额定值？2.若要把电路功率因数提高到若要把电路功率因数提高到0.95，需并多大的电容器？，需并多大的电容器？3.并联电容后，发电机的电流是多大？并联电容后，发电机的电流是多大？4.并联电容后，发电机还可接多少只并联电容后，发电机还可接多少只220V、40W的灯泡？的灯泡？解：解：1.发电机提供的电流发电机提供的电流I1UNcos 1I1=P=80002200.6=60.6A发电机额定电流发电机额定电流INUNIN=10000220=45.45ASN发电机提供的电流超过了发电机提供的电流超过了IN，不允许。不允许。解：解：2.cos 1=0.6 1=53.6o tan 1=1.33cos=0.95 =18.2o tan =0.329C=U 2P(tan 1tan)8000=3142202(1.330.329)=526F3.并联电容并联电容C后，发电机的电流后，发电机的电流IUNcos I=P=80002200.95=38.3A4.uii1iCCiNRL+iDcos=0.95 =18.2o Q=UIsin=220 38.3sin 18.2o=2631varS=P2+Q2=10000=(8000+40N)2+26312N=41盏盏3.7.1 3.7.1 串联谐振串联谐振串联谐振串联谐振串联谐振条件串联谐振条件Z=R+jX=R+j(XL-XC）当当XL=XC串联谐振频率串联谐振频率CRLuRuLuciu+或或 2 f L=12 f Cf0=2LC1f=3.7 3.7 电路中的谐振电路中的谐振电路中的谐振电路中的谐振在含有电感和电容的交流电路中，若调节电路的参数或电在含有电感和电容的交流电路中，若调节电路的参数或电源的 频率，使电路中的电流与电 源电压同相位，称这时电路中源的 频率，使电路中的电流与电 源电压同相位，称这时电路中发生了发生了谐振谐振现象。现象。按发生谐振电路的不同，谐振现象分为按发生谐振电路的不同，谐振现象分为串联谐振串联谐振和和并联谐振并联谐振。串联谐振电路的特征串联谐振电路的特征I00fI0fR1 C LZ(1)阻抗模最小阻抗模最小,为为R。电路电流最大，为电路电流最大，为U/R。(3)电感和电容两端的电压大小相等，相位相反。当电感和电容两端的电压大小相等，相位相反。当XL=XCR时，电路中将出现分电压大于总电压的现象。时，电路中将出现分电压大于总电压的现象。f0f0(2)电路呈电阻性电路呈电阻性,电源供给电电源供给电路的能量全部被电阻消耗掉。路的能量全部被电阻消耗掉。IUURUCUL(4)P=UIcos=UI=I2RQ=UIsin=03.7.1 3.7.1 串联谐振串联谐振串联谐振串联谐振串联谐振曲线串联谐振曲线f00fII01I02容性容性感性感性R2R1R2 R1Q=串联谐振电路的串联谐振电路的品质因数品质因数Q|QL(或或QC)|PUC=UL=QU=0L表明电路谐振的表明电路谐振的程度，无量纲。程度，无量纲。R=R 0C1R1 L/C=0fII00.707I0f0f2f1通频带通频带f2f1串联谐振又称电压谐振。串联谐振又称电压谐振。3.7.1 3.7.1 串联谐振串联谐振串联谐振串联谐振例例3.7.1 图示为某收音机的接收电路，已知电感图示为某收音机的接收电路，已知电感L2=250 H，其导线电阻，其导线电阻R=20。（。（1）如果天线上接收的信号有三个，其频率分别为）如果天线上接收的信号有三个，其频率分别为f1=820kHz、f2=620kHz、f3=1200kHz。若要接收。若要接收 f1=820kHz信号节目，电容器的电容信号节目，电容器的电容C 应调到多大？应调到多大？（2）如果接收到的三个信号幅值均为）如果接收到的三个信号幅值均为10 V，在电容调变到对，在电容调变到对f1发生谐振时，在发生谐振时，在L2中产生的三个信号电流各是多少毫安？频率为中产生的三个信号电流各是多少毫安？频率为f1的信号在电感的信号在电感L2上产生的电压是多少伏？上产生的电压是多少伏？L3L2L1C解：解：1.C=150 pF 1 C1 1 L2=要收听频率为要收听频率为f1信号的节目应该使谐振电路对信号的节目应该使谐振电路对f1发生谐振，即发生谐振，即f/Hz8201036201031200103XLXCZI=U/Z 12901290200.5 A100016606600.015189088510000.01UL=(XL/R)U=645 V频率为频率为 f2 和和 f3的信号在电感上的电压不到的信号在电感上的电压不到30 V，而频率为，而频率为 f1信的号则放大了信的号则放大了64.5倍倍2.当当C=150 pF，L2=250 H时，时，L2C 电路对三种信号的电抗值不同，如下表所示电路对三种信号的电抗值不同，如下表所示L3L2L1CICIILIR=+iRiLiCCRLiu+UR1=+j XL1j XC1（+）U=）R1+XC1XL1j（Y=R1+XC1XL1j（）（）XC并联谐振条件：并联谐振条件：1XL1=0Y=R1并联谐振频率并联谐振频率3.7.2 3.7.2 并联谐振并联谐振并联谐振并联谐振f0=2LC1f=1.R、L、C 并联谐振电路并联谐振电路并联谐振电路特征并联谐振电路特征(2)电流电流I为最小值，为最小值，I0=U/R(1)电路呈电阻性，电路呈电阻性，Y 最小，最小，Z 最大。最大。(3)支路电流可能会大于总电流。支路电流可能会大于总电流。0ff0I所以并联谐振又称电流谐振。所以并联谐振又称电流谐振。Q=ILI0 0 CR1 L=R=Q 值越大，谐振时阻抗模越大，选择性也就越强。值越大，谐振时阻抗模越大，选择性也就越强。I01.R、L、C 并联谐振电路并联谐振电路CII=11sin 22221)2(LfRUXRUIL+=+=+=+=22221)2(2sinLfRLfXRXLL+=+=+=+=CUfXUICC2=发生谐振时的相量图发生谐振时的相量图由相量图可得由相量图可得由于由于220121LRLCff=可得可得谐振频率谐振频率UI1ICI1 2.电感线圈和电容器并联谐振电路电感线圈和电容器并联谐振电路LuCR+ii1iC通常线圈电阻通常线圈电阻R很小，所以在谐振时很小，所以在谐振时LCff210=220121LRLCff=CII?1IIIC 10 ILfR02 901 电感线圈和电容器电感线圈和电容器并联谐振具有下列特征：并联谐振具有下列特征：1 故，谐振频率可近似等于故，谐振频率可近似等于（1）由于）由于LfR02 故故（2）电路对电源呈电阻性。）电路对电源呈电阻性。UI1ICI（3）支路电流可能会大于）支路电流可能会大于总电流。所以并联谐振总电流。所以并联谐振又称电流谐振。又称电流谐振。LuCR+ii1iC