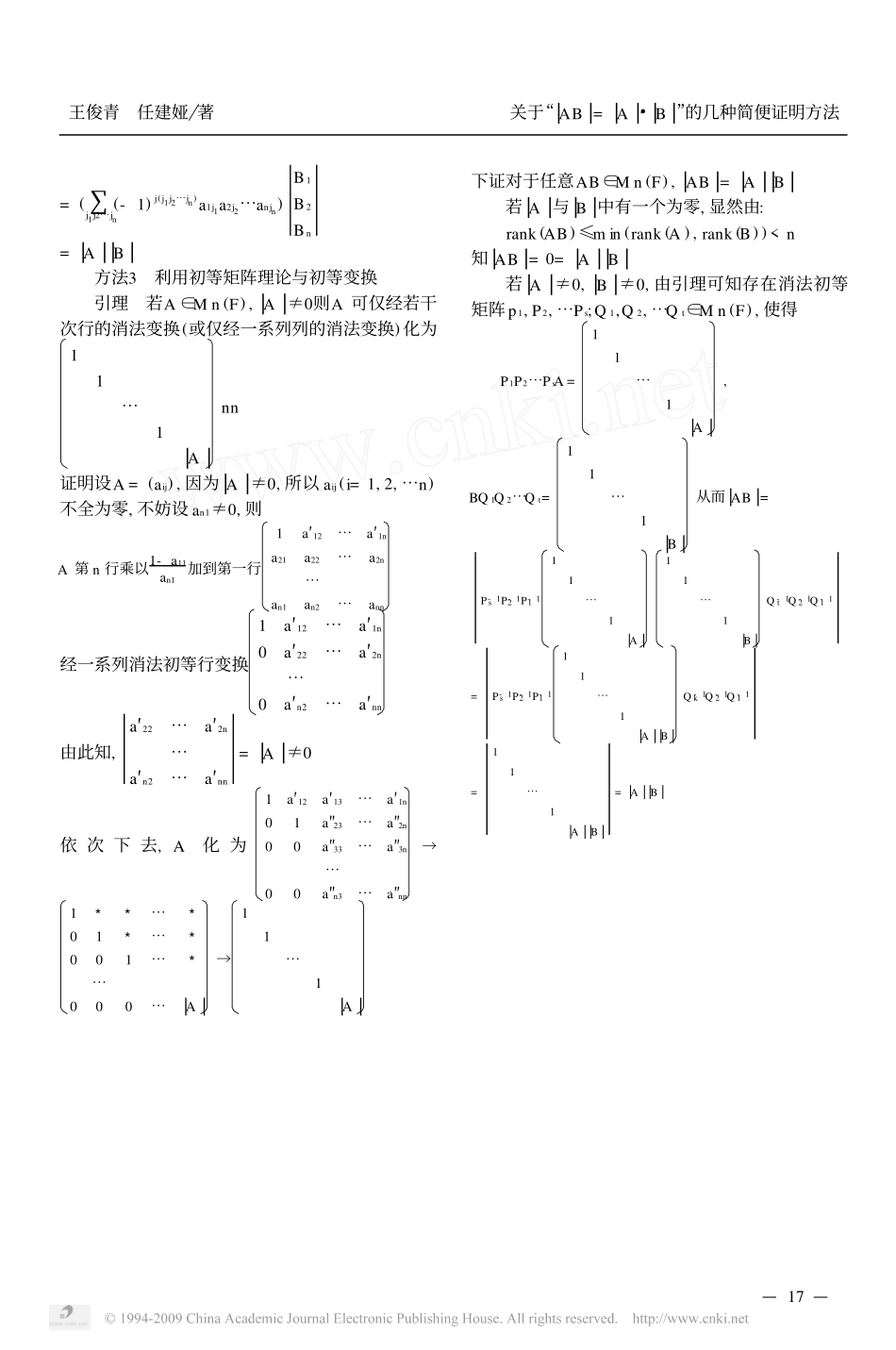
第21卷第2期2001年5月承德民族师专学报JournalofChengdeTeachersCollegeforNationalitiesVol.21No.2May.2001[收稿日期]2000-10-17[作者简介]王俊青(1960-),女,山东省德州师专数学系副教授。关于“�AB�=�A���B�”的几种简便证明方法王俊青1,任建娅2(1.山东德州高等专科学校,山东德州2530002.承德民族师专教务处,河北承德067000)[摘要]关于“矩阵积的行列式等于矩阵行列式之积”的证明,在教科书中一般采用Laplace定理给出行列式相乘规则,结合矩阵相乘的定义来进行证明,本文给出证明“�AB�=�A���B�”的三种简便方法。[关键词]分块矩阵;初等变换;初等矩阵[中图分类号]O151.21[文献标识码]A[文章编号]1005-1554(2001)02-016-02定理设A与B都是数域F上的n级方阵,则�AB�=�A���B�。证明方法1构造分块矩阵AO-IB(1)这个矩阵的行列式等于�A���B�。为了与�AB�联系我们把分块矩阵(1)的第二块行的A倍加到第一块行上,而这相当于在分块矩阵(1)的左边乘上一个相应的分块初等矩阵,即IAOIAO-IB=OAB-IB(2)右边矩阵的行列式为OAB-IB=�AB�(21)(1+2+⋯+n)+[(1+n)+⋯+2n]�2I�=�AB�(-1)n2(-1)n�I�=�AB�下面计算(2)式左边的行列式,分析IAOI=10⋯0a11a12⋯a1n01⋯0a21a22⋯a2n00⋯1an1an2⋯ann00⋯010⋯0⋯00⋯⋯⋯⋯⋯I经一系列消法初等行变换经一系列消法初等行变换10⋯000⋯001⋯000⋯0⋯00⋯100⋯0⋯00⋯I=I于是PtPt-1⋯P2P1I=IAOI,其中Pi(i=1,2,⋯t)为消法初等矩阵。因此,(2)式左边的行列式为:Pt⋯P2P1IAO-IB=Pt⋯p2p1AO-IB=AO-IB=�A��B�方法2设A=(aij),B的各行依次为B1,B2,⋯Bn于是AB=a11B1+a12B2+⋯+a1nBna21B1+a22B2+⋯+a2nBnan1B1+an2B2+⋯+annBn由行列式的性质,上式右边矩阵的行列式可以写成nn个行列式之和,易见�AB�=∑j1j2⋯jna1j1Bj1a2j2Bj2anjnBjn其中j1j2⋯jn为1,2,⋯n的全排列,则�AB�=∑j1j2⋯jnaij1a2j2⋯anjnBj1Bj2Bjn—61—王俊青任建娅�著关于“�AB�=�A���B�”的几种简便证明方法=(∑j1j2⋯jn(-1)j(j1j2⋯jn)a1j1a2j2⋯anjn)B1B2Bn=�A��B�方法3利用初等矩阵理论与初等变换引理若A∈Mn(F),�A�≠0则A可仅经若干次行的消法变换(或仅经一系列列的消法变换)化为11⋯1�A�nn证明设A=(aij),因为�A�≠0,所以aij(i=1,2,⋯n)不全为零,不妨设an1≠0,则A第n行乘以1-a11an1加到第一行1a′12⋯a′1na21a22⋯a2n⋯an1an2⋯ann经一系列消法初等行变换1a′12⋯a′1n0a′22⋯a′2n⋯0a′n2⋯a′nn由此知,a′22...