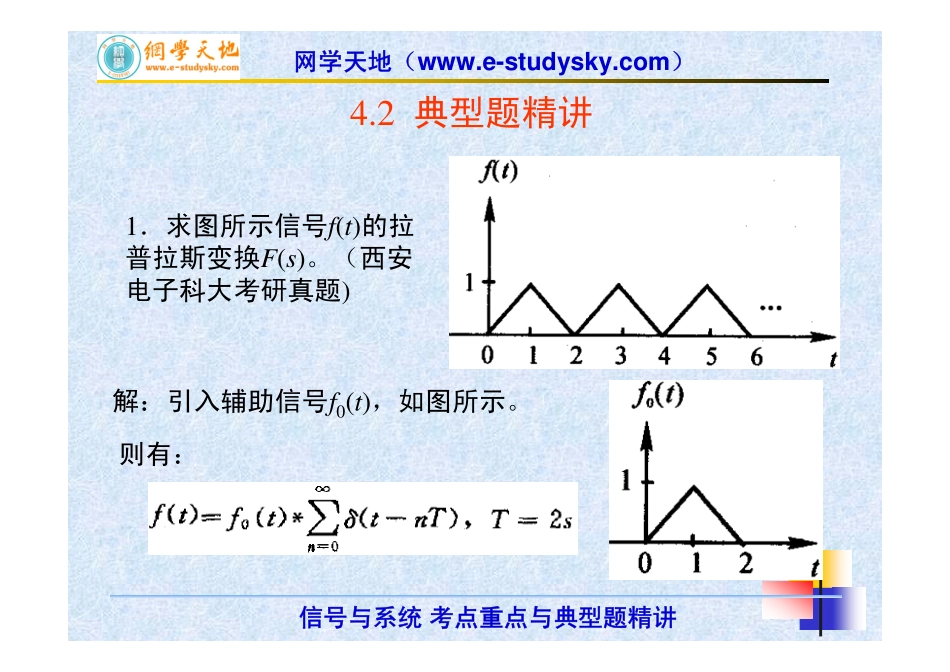
第4拉普拉斯变换、连续时间系统s域变换信号与系统考点重点与典型题精讲系列主讲人:马圆圆网学天地www.e-studysky.com网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲4.2典型题精讲1.求图所示信号f(t)的拉普拉斯变换F(s)。(西安电子科大考研真题)解:引入辅助信号f0(t),如图所示。则有:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲因为:所以:则根据拉普拉斯变换时域卷积性质得:根据拉普拉斯变换的积分性质有:又因为:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲2.判断下面的叙述是否正确:(1)一个信号存在拉普拉斯变换,就一定存在傅里叶变换。解:不正确。若拉普拉斯变换的收敛域不包含jω轴,则其傅里叶变换就不存在。(2)一个信号存在傅里叶变换,就一定存在单边拉普拉斯变换。解:不正确。因为若信号为反因果信号,则其傅里叶变换和双边拉普拉斯变换均可能存在,但单边拉普拉斯变换为零,即不存在。(3)一个信号存在傅里叶变换,就一定存在双边拉普拉斯变换。解:正确。因为傅里叶变换是双边拉普拉斯变换的特例,傅里叶变换存在,说明收敛域包含jω轴。网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲3.填空题。网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲上述两式哪个对?网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲解:(1)题图电路的s域电路模型如图所示。可得:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲当激励2sin2t单独作用时,由于是正弦稳态响应,故:所以有:故根据叠加定理得:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲5.当系统的激励f(t)=δ(t)+δ(t-1)时,系统的零状态响应为y(t)=U(t)-U(t-1)。求系统的单位阶跃响应g(t),并画出g(t)的波形。故系统函数为又因为,所以:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲经反变换得:y(t)与g(t)的的波形。网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲6.如图所示系统,网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲由此:(2)因此:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲7.已知系统函数解:根据已知的H(s)可写出系统的微分方程:对等号两端同时求单边拉普拉斯变换:网学天地(www.e-studysky.com)信号与系统考点重点与典型题精讲...