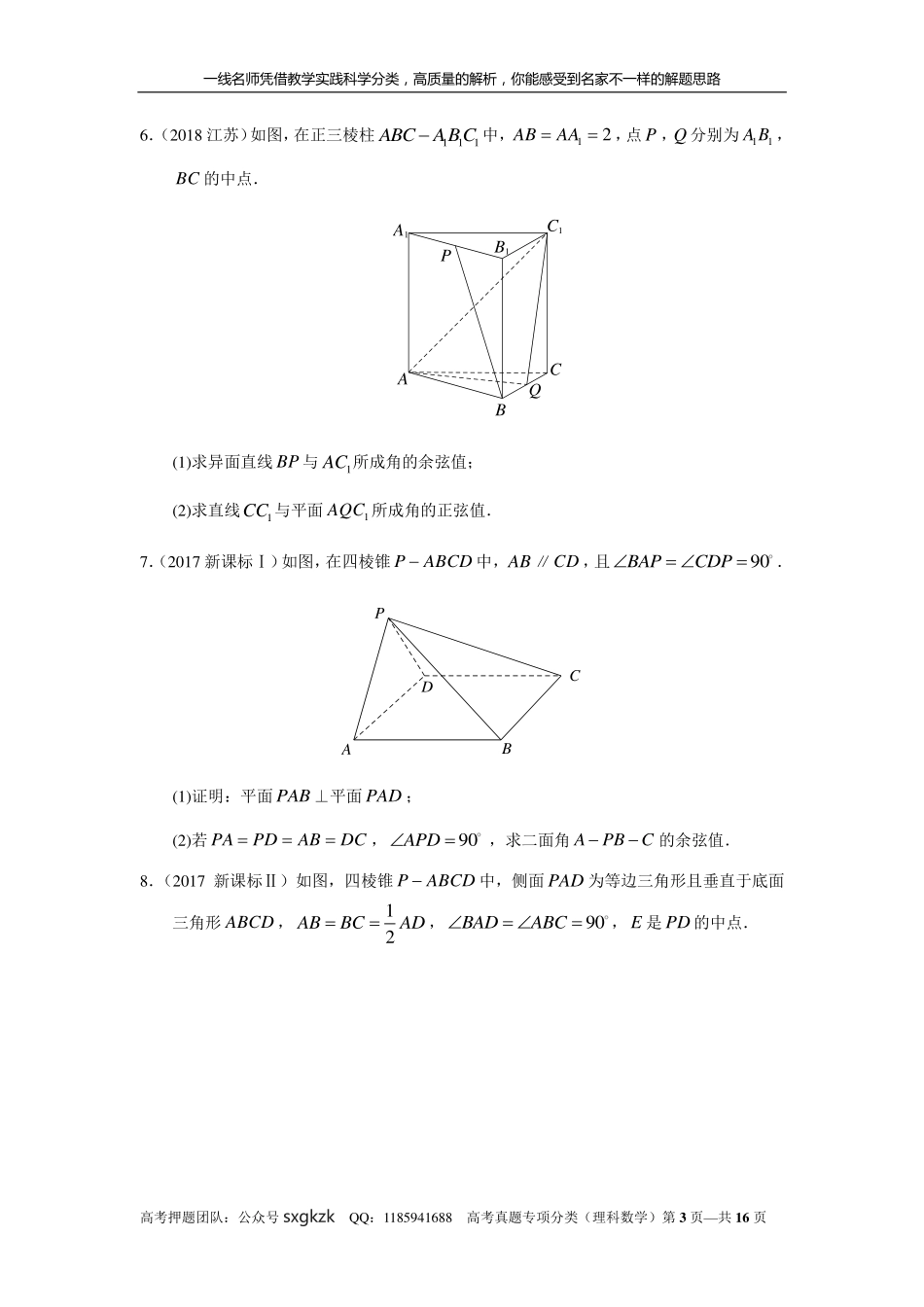
一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第1页—共16页专题八立体几何第二十四讲空间向量与立体几何解答题1.(2018全国卷Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把DFC△折起,使点C到达点P的位置,且PFBF.(1)证明:平面PEF平面ABFD;(2)求DP与平面ABFD所成角的正弦值.PFEDCBA2.(2018北京)如图,在三棱柱111ABCABC中,1CC平面ABC,D,E,F,G分别为1AA,AC,11AC,1BB的中点,5ABBC,12ACAA.C1B1A1GFEDCBA(1)求证:AC⊥平面BEF;(2)求二面角1BCDC的余弦值;(3)证明:直线FG与平面BCD相交.3.(2018全国卷Ⅱ)如图,在三棱锥PABC中,22ABBC,PAPBPC4AC,O为AC的中点.(1)证明:PO平面ABC;一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第2页—共16页(2)若点M在棱BC上,且二面角MPAC为30,求PC与平面PAM所成角的正弦值.OMPCBA4.(2018全国卷Ⅲ)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD平面BMC;(2)当三棱锥MABC体积最大时,求面MAB与面MCD所成二面角的正弦值.MDCBA5.(2018天津)如图,ADBC∥且2ADBC,ADCD,EGAD∥且EGAD,CDFG∥且2CDFG,DG平面ABCD,2DADCDG.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角EBCF的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60,求线段DP的长.NABCDEFGM一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第3页—共16页6.(2018江苏)如图,在正三棱柱111ABCABC中,12ABAA,点P,Q分别为11AB,BC的中点.ABCQPA1C1B1(1)求异面直线BP与1AC所成角的余弦值;(2)求直线1CC与平面1AQC所成角的正弦值.7.(2017新课标Ⅰ)如图,在四棱锥PABCD中,AB∥CD,且90BAPCDP.DCBAP(1)证明:平面PAB⊥平面PAD;(2)若PAPDABDC,90APD,求二面角APBC的余弦值.8.(2017新课标Ⅱ)如图,四棱锥PABCD中,侧面PAD为等边三角形且垂直于底面三角形ABCD,12ABBCAD,90BADA...