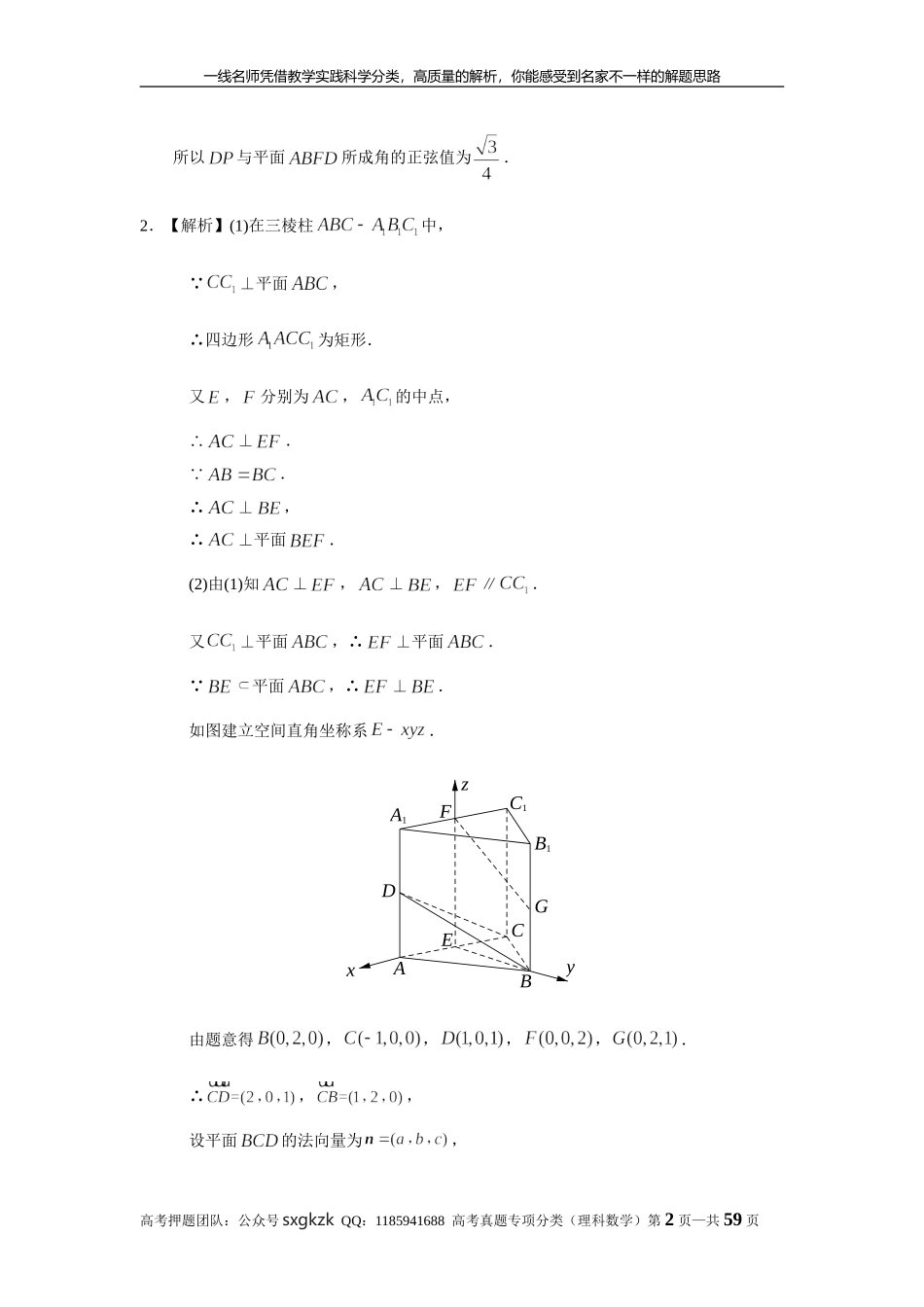
一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路专题八立体几何第二十四讲空间向量与立体几何答案部分1.【解析】(1)由已知可得,⊥,⊥,所以⊥平面PEF.又平面,所以平面⊥平面.(2)作⊥,垂足为.由(1)得,⊥平面.以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系.HzyxPFEDCBA由(1)可得,⊥.又=2,=1,所以=.又=1,=2,故⊥.可得,.则,,,,为平面的法向量.设与平面所成角为,则.高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第1页—共59页一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路所以与平面所成角的正弦值为.2.【解析】(1)在三棱柱中, ⊥平面,∴四边形为矩形.又,分别为,的中点,∴⊥. .∴⊥,∴⊥平面.(2)由(1)知⊥,⊥,∥.又⊥平面,∴⊥平面. 平面,∴⊥.如图建立空间直角坐称系.zyxC1B1A1GFEDCBA由题意得,,,,.∴,,设平面的法向量为,高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第2页—共59页一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路∴,∴,令,则,,∴平面的法向量,又 平面的法向量为,∴.由图可得二面角为钝角,所以二面角的余弦值为.(3)平面的法向量为, ,,∴,∴,∴与不垂直,∴与平面不平行且不在平面内,∴与平面相交.3.【解析】(1)因为,为的中点,所以,且.连结.因为,所以为等腰直角三角形,且,.由知.由,知平面.(2)如图,以为坐标原点,的方向为轴正方向,建立空间直角坐标系.高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第3页—共59页一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路zyxABCPMO由已知得,,,,,,取平面的法向量.设,则.设平面的法向量为.由得,可取,所以.由已知得.所以.解得(舍去),.所以.又,所以.所以与平面所成角的正弦值为.4.【解析】(1)由题设知,平面⊥平面,交线为.因为⊥,平面,所以⊥平面,故⊥.因为为上异于,的点,且为直径,所以⊥.又=,所以⊥平面.而平面,故平面⊥平面.高考押题团队:公众号sxgkzkQQ:1185941688高考真题专项分类(理科数学)第4页—共59页一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路(2)以为坐标原点,的方向...