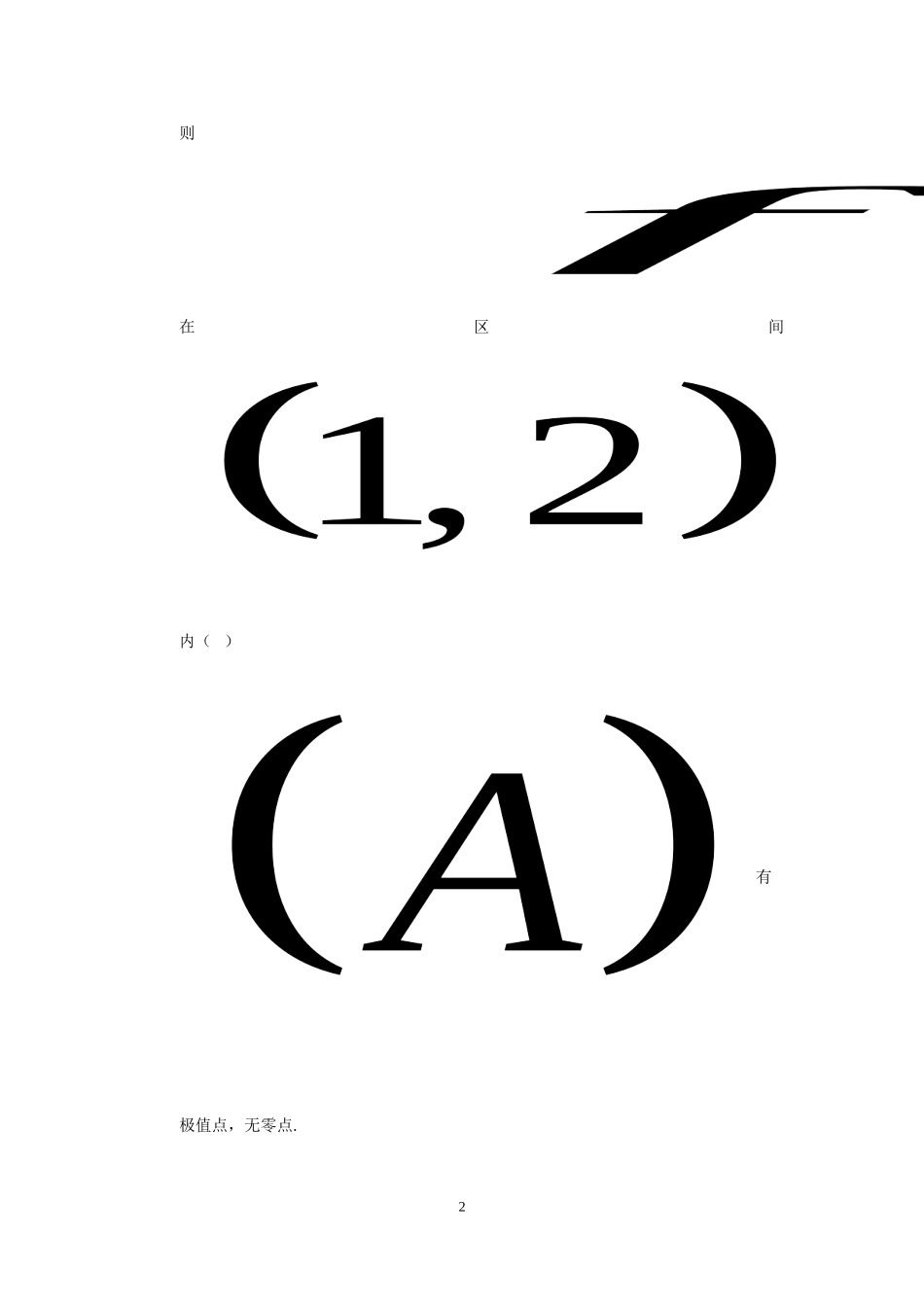2009年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)函数的可去间断点的个数,则()1.2.3.无穷多个.(2)当时,与是等价无穷小,则()....(3)设函数的全微分为,则点()不是的连续点.不是的极值点.是的极大值点.是的极小值点.(4)设函数连续,则()....(5)若不变号,且曲线在点上的曲率圆为,1则在区间内()有极值点,无零点.2无极值点,有零点.有极值点,有零点.无极值点,无零点.(6)设函数3在区间上的图形为:则函数的图形为()..41()fx-2023x-1O()fx023x1-2-11()fx023x1-2-11..(7)设、均为2阶矩阵,分别为、的伴随矩阵。若,则分块矩阵的伴随矩阵为()..5()fx023x1-11()fx023x1-2-11..6(8)设均为3阶矩阵,为的转置矩阵,且,若,则为()....二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9)曲线在处的切线方程为(10)已知,则(11)7(12)设是由方程确定的隐函数,则(13)函数在区间上的最小值为(14)设为3维列向量,为的转置,若矩阵相似于,则三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求极限(16)(本题满分10分)计算不定积分(17)(本题满分10分)设,其中具有2阶连续偏导数,求与(18)(本题满分10分)设非负函数满足微分方程,当曲线过原点时,其与直线及围成平面区域的面积为2,求绕轴旋转所得旋转体体积。(19)(本题满分10分)求二重积分,其中(20)(本题满分12分)设是区间内过的光滑曲线,当时,曲线上任一点处的法线都过原点,当时,函数满足。求的表达式(21)(本题满分11分)8(Ⅰ)证明拉格朗日中值定理:若函数在上连续,在可导,则存在,使得(Ⅱ)证明:若函数在处连续,在内可导,且,则存在,且。(22)(本题满分11分)设,(Ⅰ)求满足的所有向量(Ⅱ)对(Ⅰ)中的任一向量,证明:线性无关。(23)(本题满分11分)设二次型(Ⅰ)求二次型的矩阵的所有特征值;(Ⅱ)若二次型的规范形为,求的值。910