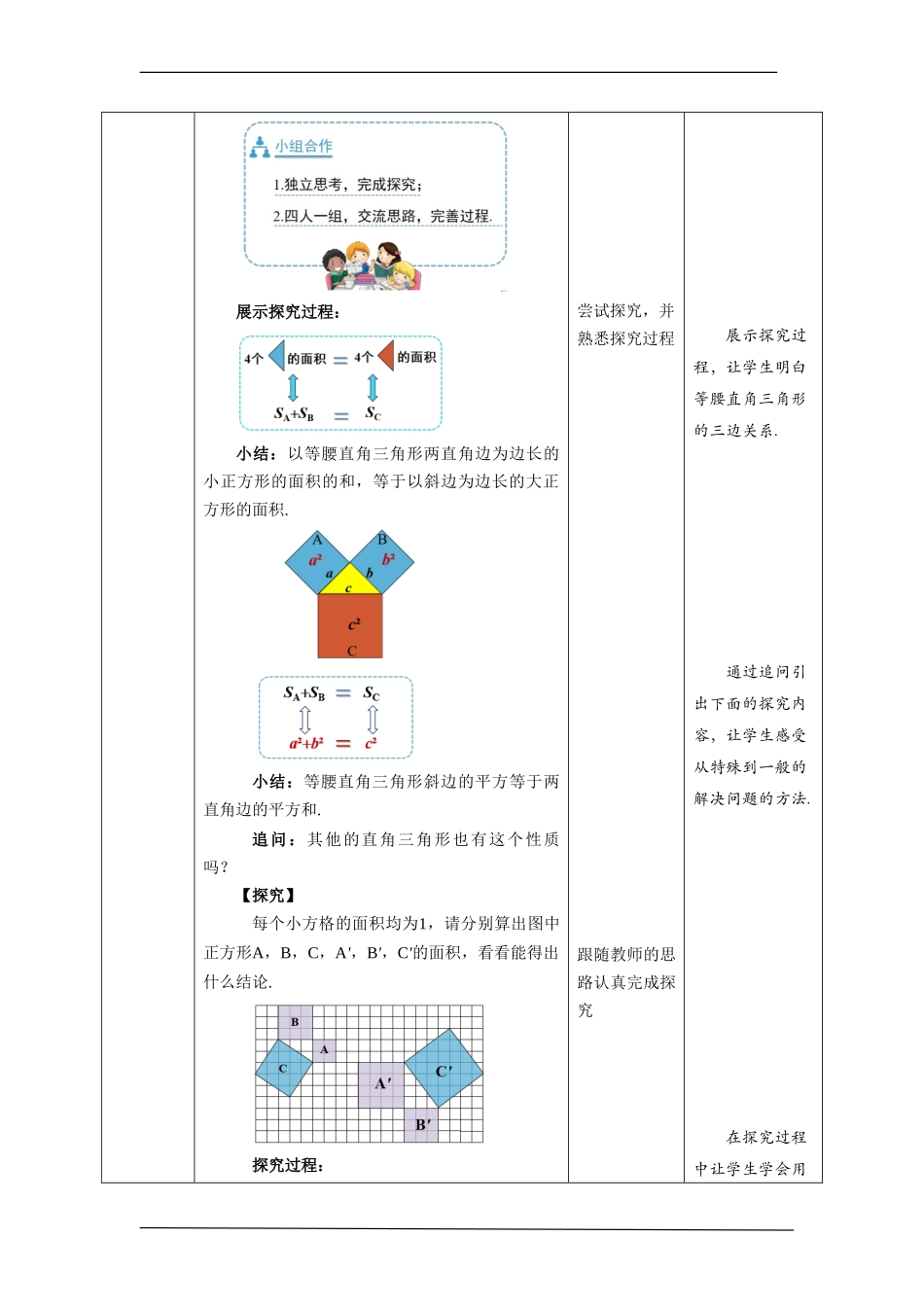
勾股定理第1课时教学设计课题勾股定理第1课时单元17学科初中数学年级八下学习目标1.掌握勾股定理,并会运用勾股定理解决一些几何问题;2.了解证明勾股定理的方法,在勾股定理的探索过程中,体会数形结合的数学思想;3.经历观察、计算、猜想、证明的过程,培养学生发现问题、分析问题和解决问题的能力;4.通过对我国古代研究勾股定理成就的介绍,培养民族自豪感;通过对勾股定理的探索和交流,培养数学学习的自信心.重点掌握勾股定理,并会运用勾股定理解决一些几何问题.难点用拼图的方法验证勾股定理.教学过程教学环节教师活动学生活动设计意图导入新课【创设情境】相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系.观察一下,你能从中发现什么数量关系吗?学生观察并思考通过情境引入,引出新课,激发学生的探索兴趣和求知欲望.垫.讲授新课【合作探究】问题:下图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?认真思考,并分组探究交流通过分组探究的形式让学生结合图形探究等腰直角三角形的三边关系,培养合作探究的意识,体会数形结合的数学思想.展示探究过程:小结:以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.小结:等腰直角三角形斜边的平方等于两直角边的平方和.追问:其他的直角三角形也有这个性质吗?【探究】每个小方格的面积均为1,请分别算出图中正方形A,B,C,A',B',C'的面积,看看能得出什么结论.探究过程:尝试探究,并熟悉探究过程跟随教师的思路认真完成探究展示探究过程,让学生明白等腰直角三角形的三边关系.通过追问引出下面的探究内容,让学生感受从特殊到一般的解决问题的方法.在探究过程中让学生学会用正方形A有4个小方格,面积为4;正方形B有9个小方格,面积为9.正方形C的面积4个直角三角形的面积小正方形的面积423113正方形C的面积大正方形的面积4个直角三角形的面积25423=13得:SASBSC.【思考】你能类比刚才的方法得出A',B',C'的面积关系吗?得:SA'SB'SC'结论:图中以直角三角形两条直角边为边长的正方形的面积的和,等于以直角三角形的斜边为边长的正方形的面积,即直角三角形两直角边的平方和等于斜边的平方.猜想:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a²b²c².认真思考并计算认真思考,积极动手剪拼,并尝...