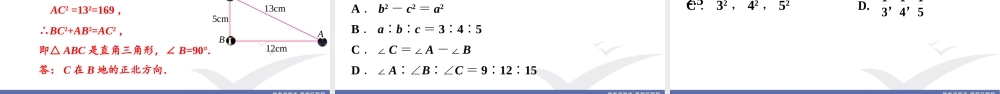第十七章勾股定理17.2勾股定理的逆定理导入新课命题1如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.条件:直角三角形的两直角边长为a,b,斜边长为c.这个命题的条件和结论分别是什么?如果将条件和结论反过来,这个命题还成立吗?结论:a2+b2=c2.探究新知据说,古埃及人曾用如图所示的方法画直角:打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.345三边分别为3,4,5,满足关系:32+42=52,则该三角形是直角三角形.画一画下面有三组数分别是一个三角形的三边长a,b,c:①5,12,13;7②,24,25;8③,15,17.0180150120906030724255131217815是问题1分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?问题2这三组数在数量关系上有什么相同点?①5,12,13满足52+122=132,a2+b2=c2①5,12,13;7②,24,25;8③,15,17.问题3由上面的几个例子,你有什么猜想呢?命题2如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.②7,24,25满足72+242=252,③8,15,17满足82+152=172.问题4命题1、命题2的题设和结论分别是什么?命题1如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.命题2如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.题设结论结论题设我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.问题5这两个命题有什么不同?1.如果三条线段长a,b,c满足a2=c2-b2,这三条线段组成的三角形是不是直角三角形?为什么?解:这三条线段组成的三角形是直角三角形.练习因为由a2=c2-b2,所以有a2+b2=c2,由勾股定理的逆定理知这个三角形是直角三角形.2.说出下列命题的逆命题.这些逆命题成立吗?内错角相等,两直线平行;如果两个实数的绝对值相等,那么这两个实数相等;(3)全等三角形的对应角相等;对应角相等的两个三角形全等;角平分线上的点到角两边的距离相等;(1)两条直线平行,内错角相等;(2)如果两个实数相等,那么它们的绝对值相等;(4)在角的内部,到角两边距离相等的点在角的平分线上.成立不成立不成立成立△ABC△△A′B′C′?∠C是直角△ABC是直角三角形ABCabc已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.求证:△ABC是直角三角形.构造两直角边分别为a,b的Rt△A′B′C...