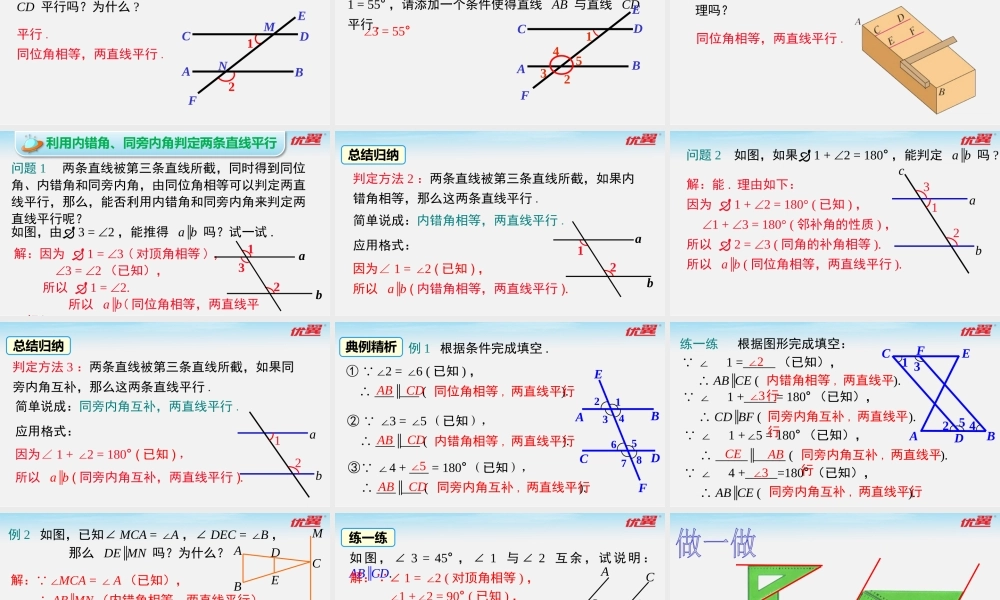
优质教学资源合集优翼与一线教师联合编写,为各位老师提供优质的原创资源,内含教学课件、教案、配套习题课件、原创模拟卷、课文朗读音视频等资料。实时更新!扫码关注!优翼七下数学教学课件(RJ)优翼第1课时平行线的判定第五章相交线与平行线5.2平行线及其判定5.2.2平行线的判定导入新课问题1两条不重合的直线的位置关系有哪几种?问题2怎样的两条直线平行?问题3上节课你学了平行线的哪些内容?相交(包括垂直)和平行两种.在同一平面内,不相交的两条直线平行.2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.1.经过直线外一点,有且只有一条直线与已知直线平行.回顾与思考思考根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?新课讲授一、放二、靠三、推四、画我们已经学习过用三角尺和直尺画平行线的方法.●利用同位角判定两条直线平行bA21aB(1)画图过程中,什么角始终保持相等?(2)直线a,b位置关系如何?思考(3)将其最初和最终的两种特殊位置抽象成几何图形:12l2l1AB(4)由上面的操作过程,你能发现判定两直线平行的方法吗?判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.应用格式:因为∠1=2∠(已知),所以l1∥l2(同位角相等,两直线平行).12l2l1AB总结归纳实验验证点击视频开始播放→练习:下图中若∠1=55°,∠2=55°,直线AB、CD平行吗?为什么?平行.同位角相等,两直线平行.ACEFBD12变式1:如图,∠1=55°,∠2=125°,直线AB与CD平行吗?为什么?ACEFBD12MN平行.同位角相等,两直线平行.变式2:如图,直线AB与CD被直线EF所截,∠1=55°,请添加一个条件使得直线AB与直线CD平行.∠3=55°ACEFBD13254你能说出木工师傅用图中的角尺工具画平行线的道理吗?练一练同位角相等,两直线平行.问题1两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?如图,由3=2,能推得a∥b吗?试一试.解:因为1=3(对顶角相等),3=2(已知),所以1=2.所以a∥b(同位角相等,两直线平行)2ba13利用内错角、同旁内角判定两条直线平行判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两...