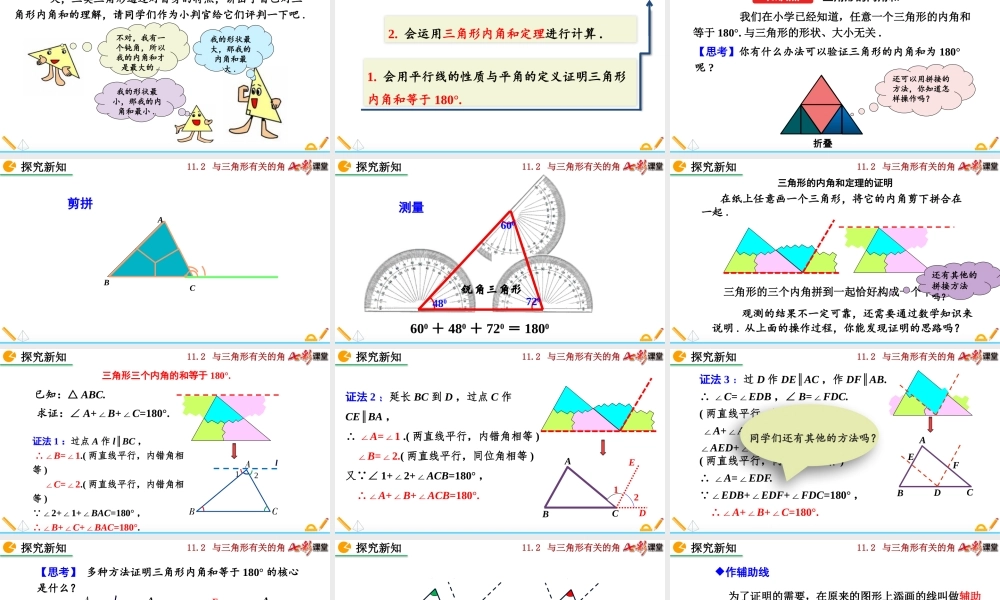
11.2与三角形有关的角/11.2与三角形有关的角11.2.1三角形的内角(第1课时)人教版数学八年级上册11.2与三角形有关的角/我的形状最小,那我的内角和最小.我的形状最大,那我的内角和最大.不对,我有一个钝角,所以我的内角和才是最大的.一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.导入新知11.2与三角形有关的角/2.会运用三角形内角和定理进行计算.1.会用平行线的性质与平角的定义证明三角形内角和等于180°.素养目标11.2与三角形有关的角/我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.【思考】你有什么办法可以验证三角形的内角和为180°呢?折叠还可以用拼接的方法,你知道怎样操作吗?探究新知知识点三角形的内角和11.2与三角形有关的角/剪拼ABC21探究新知11.2与三角形有关的角/测量480720600600+480+720=1800探究新知锐角三角形11.2与三角形有关的角/三角形的三个内角拼到一起恰好构成一个平角.观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?三角形的内角和定理的证明在纸上任意画一个三角形,将它的内角剪下拼合在一起.探究新知还有其他的拼接方法吗?11.2与三角形有关的角/l三角形三个内角的和等于180°.求证:∠A+∠B+∠C=180°.已知:△ABC.证法1:过点A作lBC∥,∴∠B=1∠.(两直线平行,内错角相等)∠C=2∠.(两直线平行,内错角相等) ∠2+1+∠∠BAC=180°,∴∠B+∠C+∠BAC=180°.12探究新知11.2与三角形有关的角/证法2:延长BC到D,过点C作CEBA∥,∴∠A=1∠.(两直线平行,内错角相等)∠B=2.∠(两直线平行,同位角相等)又 ∠1+2+∠∠ACB=180°,∴∠A+∠B+∠ACB=180°.CBAED12探究新知11.2与三角形有关的角/CBAEDF证法3:过D作DE∥AC,作DF∥AB.∴∠C=∠EDB,∠B=∠FDC.(两直线平行,同位角相等)∠A+∠AED=180°,∠AED+∠EDF=180°,(两直线平行,同旁内角相补)∴∠A=∠EDF. ∠EDB+∠EDF+∠FDC=180°,∴∠A+∠B+∠C=180°.探究新知同学们还有其他的方法吗?11.2与三角形有关的角/【思考】多种方法证明三角形内角和等于180°的核心是什么?借助平行线的“移角”的功能,将三个角转化成一个平角.借助平行线的“移角”的功能,将三个角转化成一个平角.探究新知l12CBAED12CBAEDF11.2与三角形有关的角/C24AB3EQDFPGH1BGC24A3EDFH1同学们按照上图中的辅助线,给出证明步骤.探究新知试一试11.2...