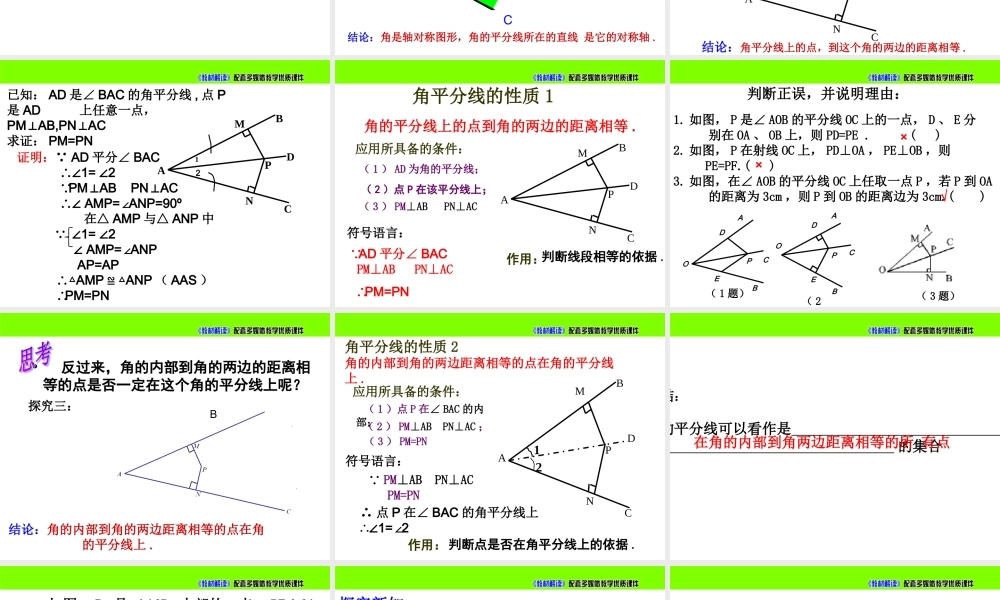
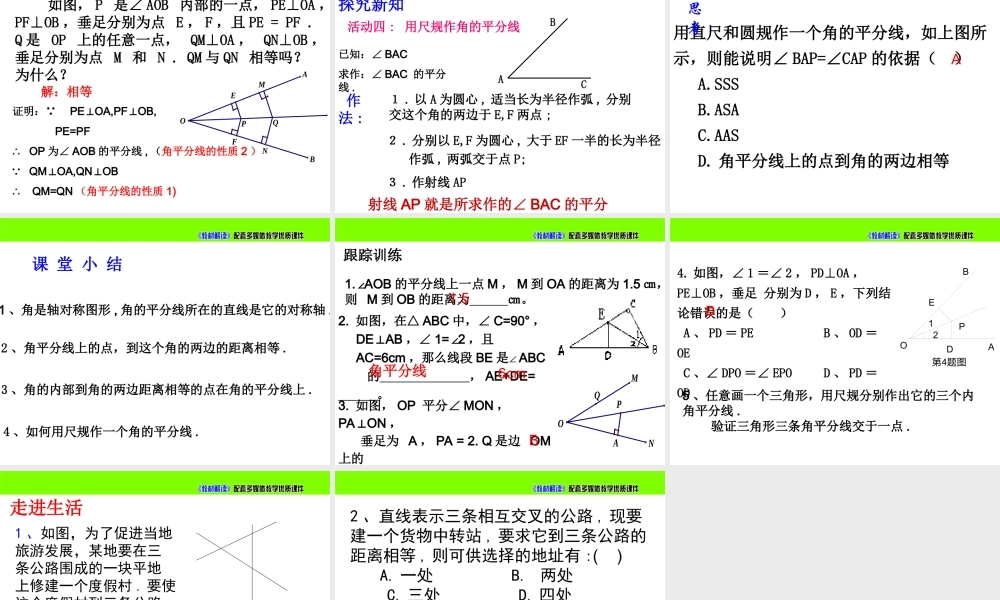
知识回顾1、角平分线的概念一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.oBCA12符号语言: 射线OC是∠AOB的角平分线∴∠1=∠2知识回顾2、点到直线距离:从直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离.OPAB垂线段PO的长度以看做是学过的集合定义:线段垂直平分线可以看做是的集合到定点距离等于定长的所有点到线段两端点的距离相等的所有点在纸上任意画一个∠BAC,把它沿经过点A的某条直线对折,使角的两边AB与AC重合,然后把纸展开后铺平,记折痕为AD.你发现∠BAC是轴对称图形吗?如果是,它的对称轴是什么?CBAD活动一:结论:角是轴对称图形,角的平分线所在的直线是它的对称轴.探究角的轴对称性探究新知请同学们在刚才折出的角平分线AD上,任意取一点P通过尺规作图,过点P作PM⊥AB,PN⊥AC,垂足分别是点M,N,用圆规比较PM与PN的大小,你有什么发现?说明你的理由.结论:角平分线上的点,到这个角的两边的距离相等.探索角平分线的第一个性质探究新知活动二:CBMAPND已知:AD是∠BAC的角平分线,点P是AD上任意一点,PMAB,PNAC⊥⊥求证:PM=PNCBMAPND12证明: AD平分∠BAC∴∠1=∠2 PMABPNAC⊥⊥∴∠AMP=∠ANP=90º在△AMP与△ANP中 ∠1=∠2∠AMP=∠ANPAP=AP∴△AMP≌△ANP(AAS)∴PM=PN角平分线的性质1角的平分线上的点到角的两边的距离相等.CBMAPND应用所具备的条件:(1)AD为角的平分线;(2)点P在该平分线上;(3)PM⊥ABPN⊥AC作用:判断线段相等的依据.符号语言: AD平分∠BACPM⊥ABPN⊥AC∴PM=PN判断正误,并说明理由:1.如图,P是∠AOB的平分线OC上的一点,D、E分别在OA、OB上,则PD=PE.()2.如图,P在射线OC上,PD⊥OA,PE⊥OB,则PE=PF.()3.如图,在∠AOB的平分线OC上任取一点P,若P到OA的距离为3cm,则P到OB的距离边为3cm.()AOBCDEPPEDCBOA(1题)(2(3题)×√ו反过来,角的内部到角的两边的距离相等的点是否一定在这个角的平分线上呢?B结论:角的内部到角的两边距离相等的点在角的平分线上.探究三:角平分线的性质2角的内部到角的两边距离相等的点在角的平分线上.应用所具备的条件:(1)点P在∠BAC的内部;(2)PM⊥ABPN⊥AC;(3)PM=PN作用:判断点是否在角平分线上的依据.符号语言: PM⊥ABPN⊥ACPM=PN∴点P在∠BAC的角平分线上∴∠1=2∠CBMAPND12结:的平分线可以看作是的集合在角的内部到角两边距离相等的所有点如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB,垂足分别为点E,F,...