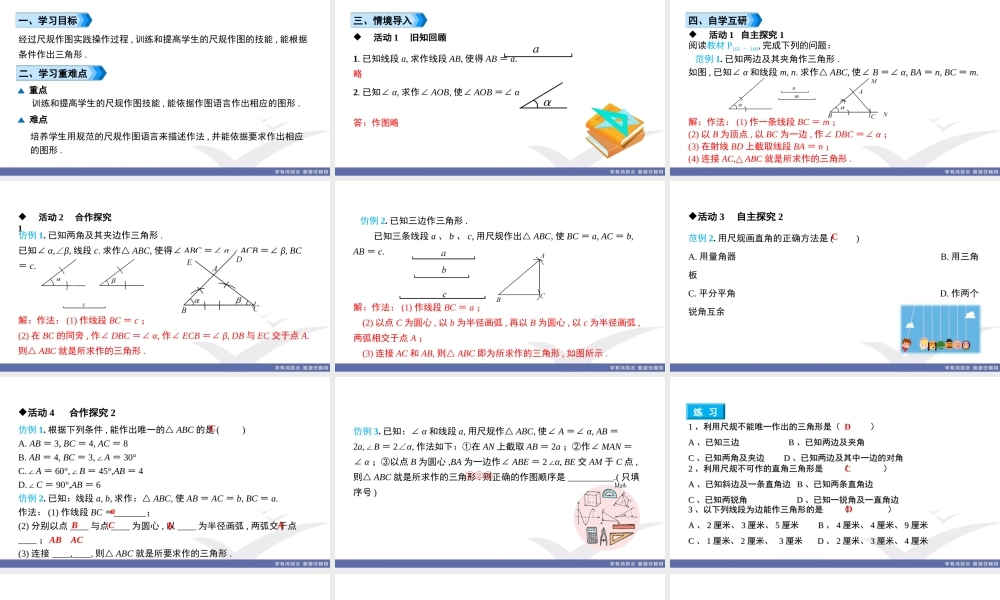
第四章三角形课题用尺规作三角形一、学习目标重点难点二、学习重难点经过尺规作图实践操作过程,训练和提高学生的尺规作图的技能,能根据条件作出三角形.训练和提高学生的尺规作图技能,能依据作图语言作出相应的图形.培养学生用规范的尺规作图语言来描述作法,并能依据要求作出相应的图形.活动1旧知回顾三、情境导入1.已知线段a,求作线段AB,使得AB=a.略2.已知∠α,求作∠AOB,使∠AOB=∠α.答:作图略活动1自主探究1四、自学互研阅读教材P105-106,完成下列的问题:范例1.已知两边及其夹角作三角形.如图,已知∠α和线段m,n.求作△ABC,使∠B=∠α,BA=n,BC=m.解:作法:(1)作一条线段BC=m;(2)以B为顶点,以BC为一边,作∠DBC=∠α;(3)在射线BD上截取线段BA=n;(4)连接AC,△ABC就是所求作的三角形.活动2合作探究1仿例1.已知两角及其夹边作三角形.已知∠α,∠β,线段c.求作△ABC,使得∠ABC=∠α,∠ACB=∠β,BC=c.解:作法:(1)作线段BC=c;(2)在BC的同旁,作∠DBC=∠α,作∠ECB=∠β,DB与EC交于点A.则△ABC就是所求作的三角形.仿例2.已知三边作三角形.已知三条线段a、b、c,用尺规作出△ABC,使BC=a,AC=b,AB=c.解:作法:(1)作线段BC=a;(2)以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;(3)连接AC和AB,则△ABC即为所求作的三角形,如图所示.活动3自主探究2范例2.用尺规画直角的正确方法是()A.用量角器B.用三角板C.平分平角D.作两个锐角互余C活动4合作探究2仿例1.根据下列条件,能作出唯一的△ABC的是()A.AB=3,BC=4,AC=8B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4D.∠C=90°,AB=6仿例2.已知:线段a,b,求作:△ABC,使AB=AC=b,BC=a.作法:(1)作线段BC=;(2)分别以点____与点____为圆心,以____为半径画弧,两弧交于点____;(3)连接____,____,则△ABC就是所要求作的三角形.CaBCbAABAC仿例3.已知:∠α和线段a,用尺规作△ABC,使∠A=∠α,AB=2a,∠B=2∠α,作法如下:①在AN上截取AB=2a;②作∠MAN=∠α;③以点B为圆心,BA为一边作∠ABE=2∠α,BE交AM于C点,则△ABC就是所求作的三角形.则正确的作图顺序是__________.(只填序号)①②③练习11、利用尺规不能唯一作出的三角形是()、利用尺规不能唯一作出的三角形是()AA、已知三边、已知三边BB、已知两边及夹角、已知两边及夹角CC、已知两角及夹边、已知两角及夹边DD、已知两边及其中一边的对角、已知两边及其中一边的对角22、利用尺规不可...