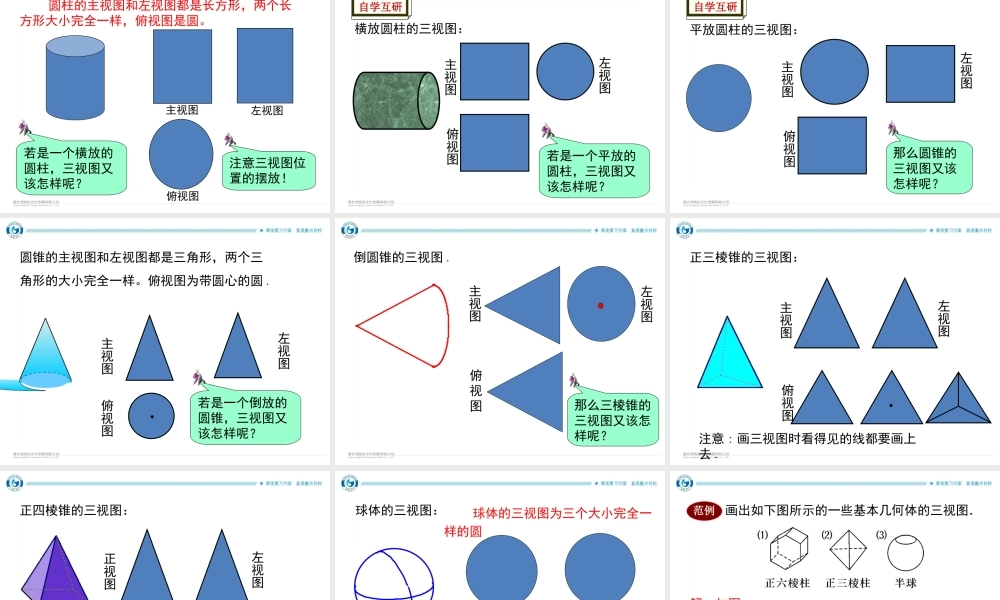
第4章图形的初步认识4.2立体图形的视图4.2.1由立体图形到视图学习目标【学习目标】1.让学生了解三视图与现实生活的联系,会画简单的三视图;2.通过从不同的方向关察物体,培养学生的空间观念;3.通过观察思考,得到视图的不同效果,培养学生主动参与意识,激发学习兴趣.【学习重点】会画从不同方向观察简单物体的三视图.【学习难点】画组合体的三视图.情景导入对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.工人在建造房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.为了解决这个问题,可以采用三视图,这节课就让我们一起来研究三视图吧.T26M坦克实物摩托车自学互研知识模块一中心投影和平行投影阅读教材P123~P126,完成下面的内容.归纳:视图来自于投影,而投影又分为中心投影和平行投影.(1)________形成的投影称为中心投影;(2)_________形成的投影称为平行投影.点光源平行光线下列四幅图中,表示两棵小树在同一时刻阳光下的影子的图形可能是()范例ABCDD仿例下列投影中不属于中心投影的是()A.晚上路灯下小孩的影子B.汽车灯光照射下行人的影子C.阳光下沙滩上人的影子D.舞台上一束灯光下演员的影子C变例小明拿了一个等边三角形木框在阳光下玩,那么等边三角形木框在地面上形成的影子不可能是()ABCDB知识模块二由立体图形到视图视图是一种特殊的平行投影.从正面、上面和侧面(左面或右面)三个不同的方向进行平行投影,可以得到三个投影,这样就可以用平面图形去刻画一个立体图形了.归纳从正面得到的投影,称为______;从上面得到的投影,称为_______;从侧面得到的投影,称为______.依投影方向不同,有左视图和右视图.通常将_______、________、与__________称为一个物体的三视图.主视图俯视图侧视图主视图俯视图左(右)视图从正面得到的投影从上面得到的投影从侧面得到的投影,立体图形的三视图:主视图、俯视图、侧视图主视图:俯视图:侧视图:分左视图和右视图自学互研主视图正方体的三视图都是正方形.俯视图左视图注意三视图位置的摆放!且三个正方形的大小完全一样自学互研圆柱的主视图和左视图都是长方形,两个长方形大小完全一样,俯视图是圆。主视图左视图俯视图注意三视图位置的摆放!若是一个横放的圆柱,三视图又该怎样呢?横放圆柱的三视图:主视图俯视图左视图若是一个平放的圆柱,三视图又该怎样呢?自学互研平放圆柱的三视...