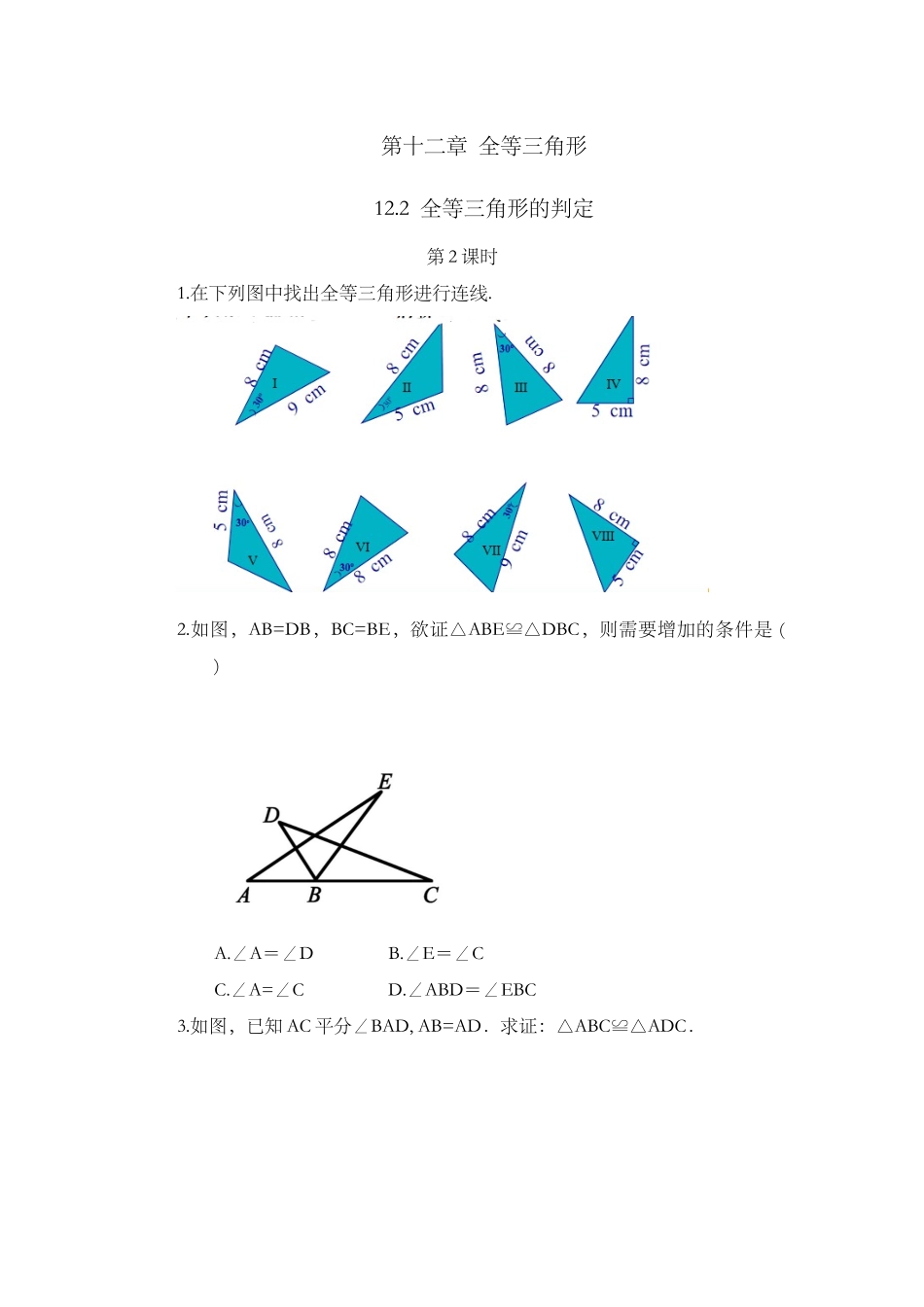
第十二章全等三角形12.2全等三角形的判定第2课时1.在下列图中找出全等三角形进行连线.2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是()A.∠A=∠DB.∠E=∠CC.∠A=∠CD.∠ABD=∠EBC3.如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.4.已知:如图,AB=AC,BD=CD,E为AD上一点.求证:BE=CE.5.如图,已知CA=CB,AD=BD,M,N分别是CA,CB的中点,求证:DM=DN.参考答案:1.答案如下:2.D3.证明:∵AC平分∠BAD,∴∠BAC=∠DAC,在△ABC和△ADC中,AD=AB(已知),∠BAC=∠DAC(已证),AC=AC(公共边),∴△ABC≌△ADC(SAS).4.证明:在△ABD和△ACD中,AB=AC(已知),BD=CD(已知),AD=AD(公共边),∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD,在△ABE和△ACE中,AB=AC(已知),∠BAD=∠CAD(已证),AE=AE(公共边),∴△ABE≌△ACE(SAS).∴BE=CE.5.证明:连接CD,如图所示;在△ABD与△CBD中CA=CB,(已知)AD=BD,(已知)CD=CD,(公共边)∴△ACD≌△BCD(SSS)∴∠A=∠B又∵M,N分别是CA,CB的中点,∴AM=BN在△AMD与△BND中AM=BN,(已证)∠A=∠B,(已证)AD=BD,(已知)∴△AMD≌△BND.(SAS)∴DM=DN.