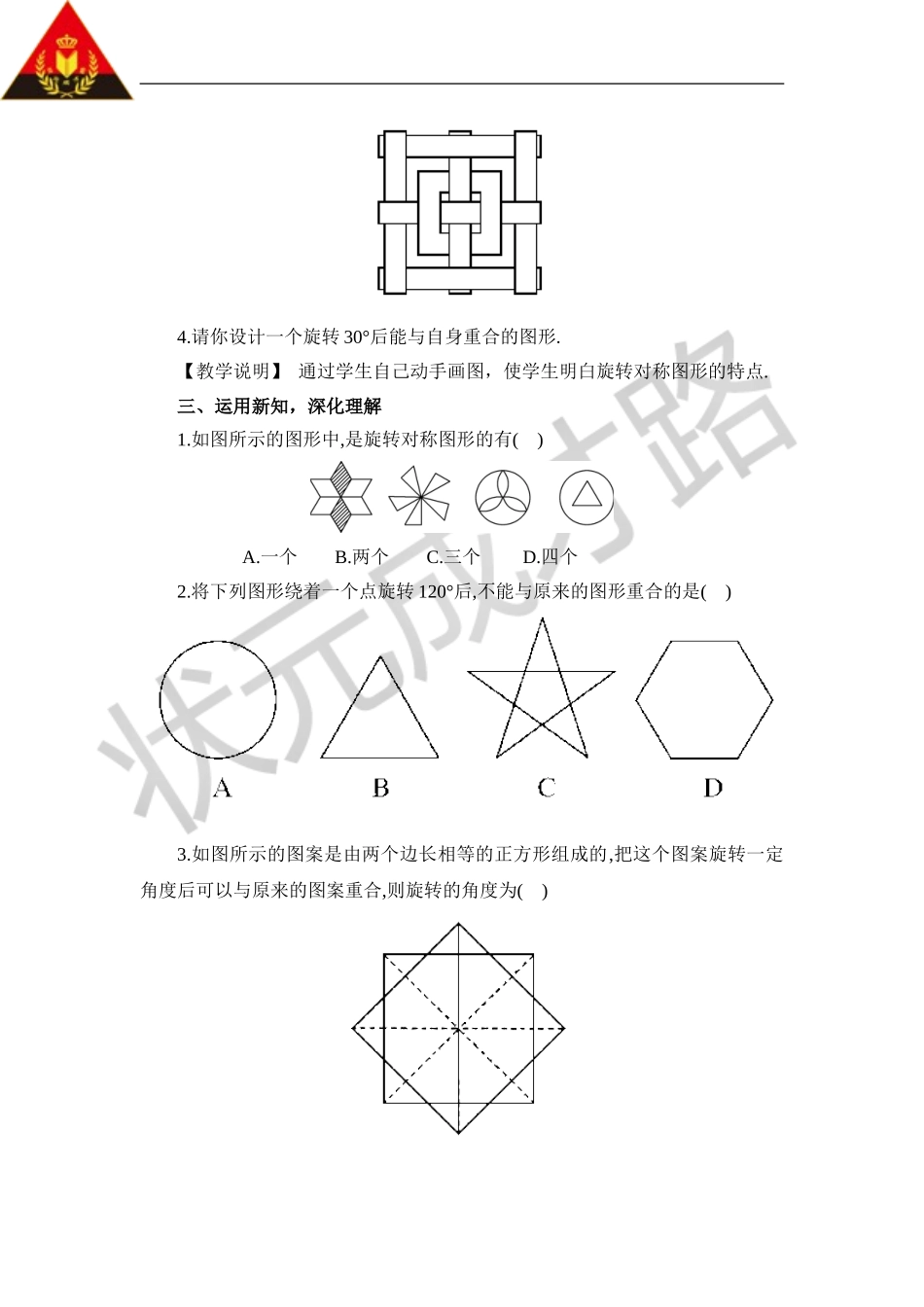
3.旋转对称图形【知识与技能】理解旋转对称图形和旋转对称的特征.【过程与方法】通过探究图形之间的变换关系的过程,发展图形的分析能力,提高“化归”意识和综合运用变换解决实际问题的能力.【情感态度】培养探究意识,感悟变换的内涵,体会其价值.【教学重点】认识旋转对称图形.【教学难点】合理运用变换解决有关问题.一、情境导入,初步认识在日常生活中,一些图形绕着某一定点转动一定的角度后能与自身重合.电扇的叶片转动°能与自身重合;螺旋桨转动°后,能与自身重合.你能再举出一些这样的实例吗?【教学说明】用生活中的现象引入本节课的内容,使学生明白数学来源于生活,应用于生活.二、思考探究,获取新知1.做一做用一张半透明的薄纸,覆盖在如图所示的图形上,在薄纸上画这个图形,使它与如图所示的图形重合.然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再一次重合.【归纳结论】图形围绕旋转中心旋转一定角度后能与自身重合的图形就称为旋转对称图形.注意:这个旋转的角度并不是唯一的.2.用类似上述的操作方法对如图所示的图形进行旋转,它是不是旋转对称图形?想一想:旋转中心在何处?该图形需要旋转多少度后,能与自身重合?该图形是轴对称图形吗?3.如图所示的图形是轴对称图形,用类似上述的操作方法对所示的图形进行探索,它能通过旋转与自身重合吗?4.请你设计一个旋转30°后能与自身重合的图形.【教学说明】通过学生自己动手画图,使学生明白旋转对称图形的特点.三、运用新知,深化理解1.如图所示的图形中,是旋转对称图形的有()A.一个B.两个C.三个D.四个2.将下列图形绕着一个点旋转120°后,不能与原来的图形重合的是()3.如图所示的图案是由两个边长相等的正方形组成的,把这个图案旋转一定角度后可以与原来的图案重合,则旋转的角度为()A.45°或90°B.90°或180°C.180°或270°D.45°n(1≤n≤8,且n为正整数)4.如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是()A.72°B.108°C.144°D.216°5.如下图案可以看做是哪个基本图形通过几次旋转得到的?每次旋转了多少度?旋转中心是哪个?6.如图,下列各图形是否是旋转对称图形?若是,则各绕哪一点最少要旋转多少度后,能与它自身重合?【教学说明】对前面所学知识进行巩固提高.【答案】1.D2.C3.D4.B5.解:图案可以看作由一个菱形通过6次旋转得到的,每次旋转60°,旋转中心在图形的中心.6.解:(1)是旋转对称图形,圆心...