14.3.2 公式法（第1课时）.pptxVIP免费

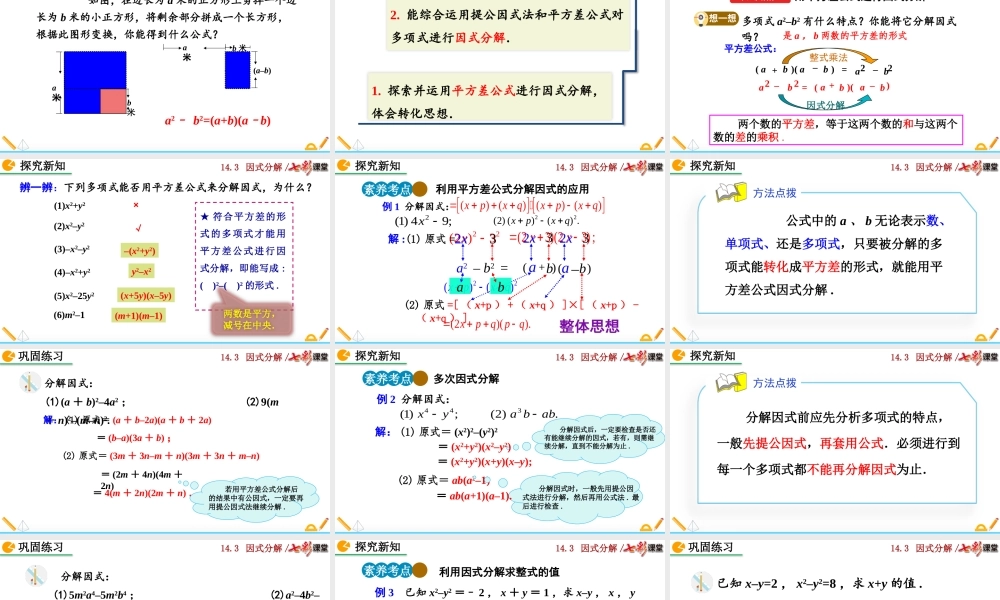
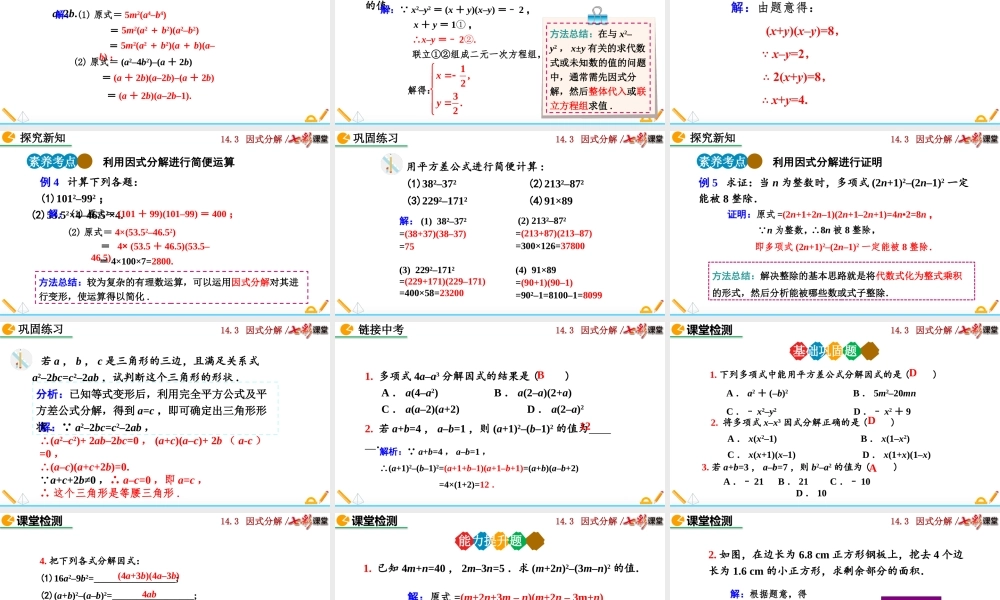
14.3因式分解/14.3因式分解14.3.2公式法(第1课时)人教版数学八年级上册14.3因式分解/a米b米b米a米(a–b)如图，在边长为a米的正方形上剪掉一个边长为b米的小正方形，将剩余部分拼成一个长方形，根据此图形变换，你能得到什么公式？a2–b2=(a+b)(a–b)导入新知14.3因式分解/1.探索并运用平方差公式进行因式分解，体会转化思想．2.能综合运用提公因式法和平方差公式对多项式进行因式分解．素养目标14.3因式分解/用平方差公式进行因式分解多项式a2–b2有什么特点？你能将它分解因式吗？是a，b两数的平方差的形式))((baba–+=22ba–))((22bababa–+=–整式乘法因式分解两个数的平方差，等于这两个数的和与这两个数的差的乘积.平方差公式：探究新知知识点想一想14.3因式分解/√√××辨一辨：下列多项式能否用平方差公式来分解因式，为什么？√√★符合平方差的形式的多项式才能用平方差公式进行因式分解，即能写成:()2–()2的形式.两数是平方，减号在中央．(1)x2+y2(2)x2–y2(3)–x2–y2–(x2+y2)y2–x2(4)–x2+y2(5)x2–25y2(x+5y)(x–5y)(6)m2–1(m+1)(m–1)探究新知14.3因式分解/2(1)49;x例1分解因式：22(2)3x(23)(23);xx22(2)()().xpxqaabb(+)(–)a2–b2=解:(1)原式=2x32x2x33()()()()xpxqxpxq(2)原式=[（x+p）+（x+q）]×[（x+p）-（x+q）](2)().xpqpq整体思想22()()xpxqab素养考点1利用平方差公式分解因式的应用探究新知14.3因式分解/方法点拨公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成平方差的形式，就能用平方差公式因式分解.探究新知14.3因式分解/分解因式：(1)(a＋b)2–4a2；(2)9(m＋n)2–(m–n)2.＝(2m＋4n)(4m＋2n)解：(1)原式＝(a＋b–2a)(a＋b＋2a)＝(b–a)(3a＋b)；(2)原式＝(3m＋3n–m＋n)(3m＋3n＋m–n)＝4(m＋2n)(2m＋n)．若用平方差公式分解后的结果中有公因式，一定要再用提公因式法继续分解.巩固练习14.3因式分解/例2分解因式：443(1);(2).xyabab解：(1)原式＝(x2)2–(y2)2＝(x2+y2)(x2–y2)分解因式后，一定要检查是否还有能继续分解的因式，若有，则需继续分解，直到不能分解为止.＝(x2+y2)(x+y)(x–y);(2)原式＝ab(a2–1)分解因式时，一般先用提公因式法进行分解，然后再用公式法.最后进行检查.＝ab(a+1)(a–1).素养考点2多次因式分解探究新知14.3因式分解/方法点拨分解因式前应先分析多项式的特点，一般先提公因式，再套用公式．必...