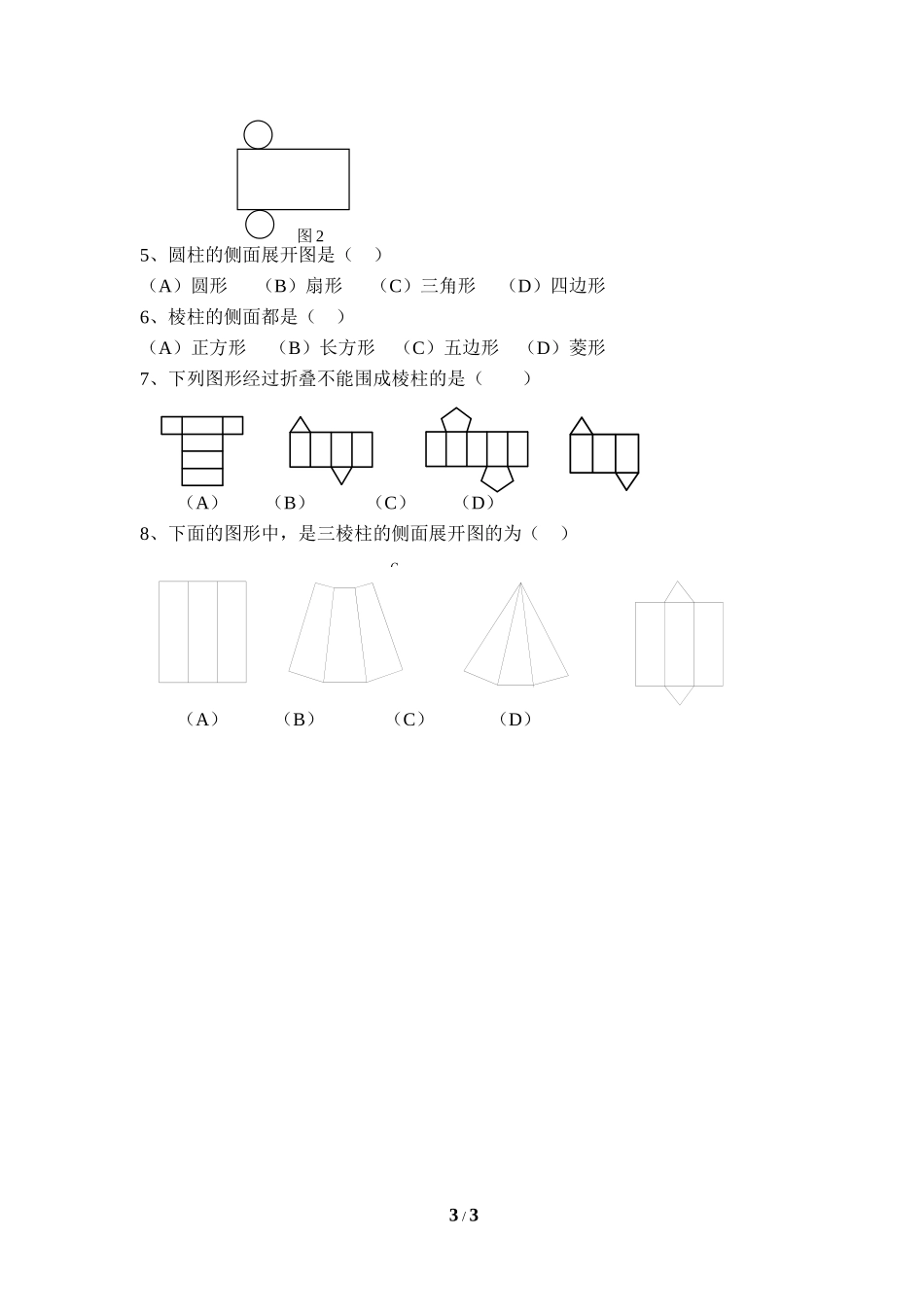
1.2展开与折叠(2)学习目标:1、在操作活动中认识棱柱的某些特性.2、了解棱柱展开图的形状,能正确地判断和制作简单的立体模型.3、经历展开与折叠、模型制作等活动,发展空间观念,积累数学活动经验.本节重点:1、认识棱柱的某些特征,形成规范的语言.2、能根据棱柱的展开图判断和制作简单的立体图形.本节难点:根据棱柱的展开图判断和操作简单的立体图形.学习过程:一、回顾与思考:1、棱柱的特点若有若干几何体,你能立刻找到棱柱吗?棱柱有什么与众不同的特征呢?(1)棱柱的上、下底面是___________________________.(2)棱柱的侧面都是______________.(3)棱柱的所有侧棱长都_____________.(4)棱柱侧面的个数与底面多图形的边数______________.(5)棱柱各元素间的数量关系如下:名称底面形状顶点数棱数侧棱数侧面数侧面形状总面数n棱柱2、棱柱的分类我们已经了解了棱柱,那么棱柱之间是否还有区别呢?通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱……长方体和正方体都是____________________.二、新课探究:将下图中的棱柱沿某些棱剪开,展开成一个平面图形,你能得到哪些形状的平面图形?1/3想一想:⑴下图中,哪些图形经过折叠可以围成一个棱柱?先想一想,再折一折.⑵将上图中不能围成棱柱的图形作适当修改使得图形能围成一个棱柱.做一做:按照课本所示的方法把圆柱、圆锥的侧面展开,会得到什么图形?先想一想,再试一试.观察圆柱形纸筒展开的侧面是一个什么图形:观察圆锥形圣诞帽的侧面是什么图形?三、课堂练习:1、如图1,折叠后是一个体;2、一个六棱柱模型,它的上、下底面的形状、大小都相同,底面边长都是5cm,侧棱长4cm,则它的所有侧面的面积之和为______;3、展开一个棱柱的侧面是,分为棱柱和棱柱;4、如图2是一个几何体的表面展成的平面图形,则这个几何体是.2/35、圆柱的侧面展开图是()(A)圆形(B)扇形(C)三角形(D)四边形6、棱柱的侧面都是()(A)正方形(B)长方形(C)五边形(D)菱形7、下列图形经过折叠不能围成棱柱的是()(A)(B)(C)(D)8、下面的图形中,是三棱柱的侧面展开图的为()(A)(B)(C)(D)3/3图2BDC