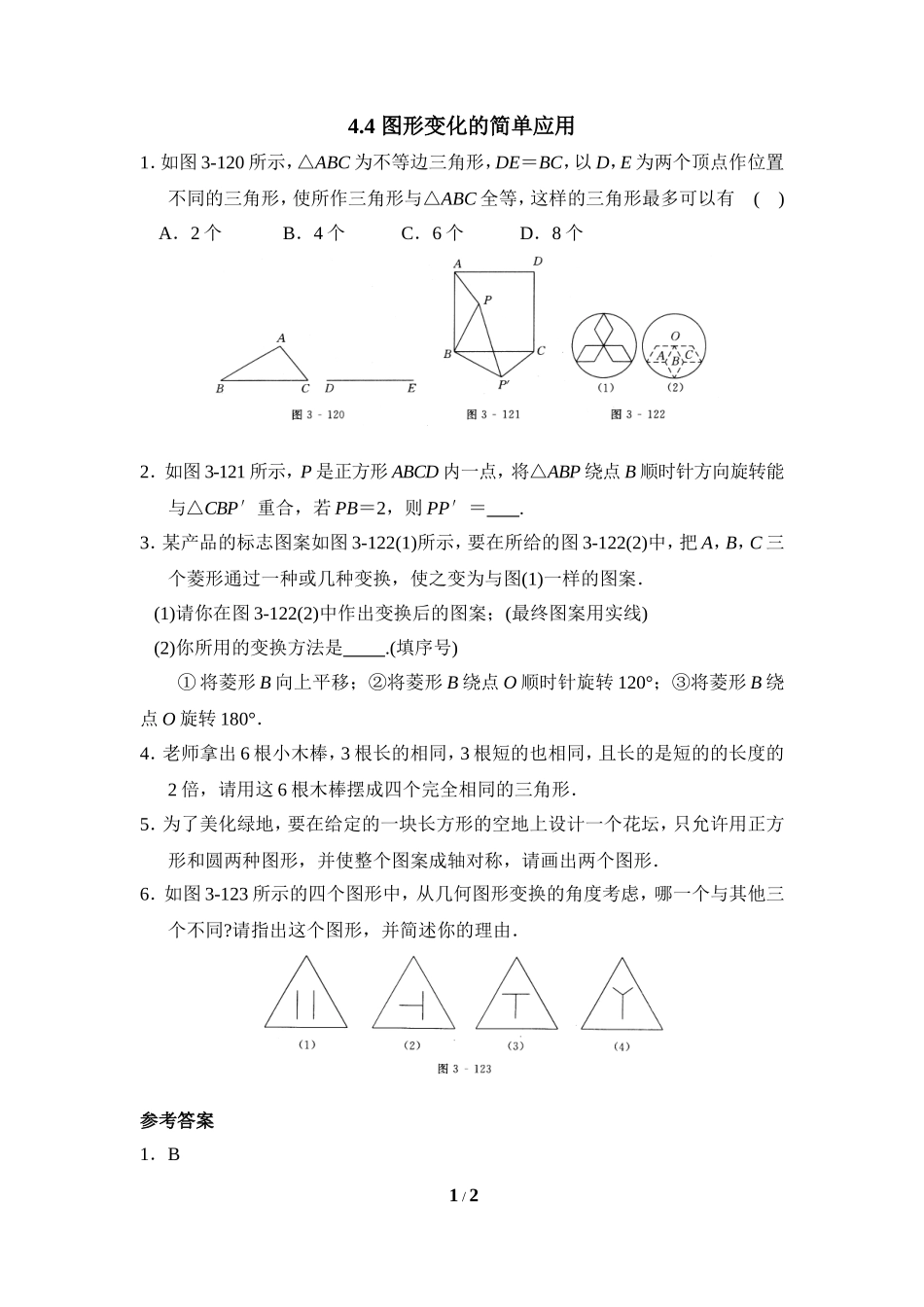
4.4图形变化的简单应用1.如图3-120所示,△ABC为不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以有()A.2个B.4个C.6个D.8个2.如图3-121所示,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=2,则PP′=.3.某产品的标志图案如图3-122(1)所示,要在所给的图3-122(2)中,把A,B,C三个菱形通过一种或几种变换,使之变为与图(1)一样的图案.(1)请你在图3-122(2)中作出变换后的图案;(最终图案用实线)(2)你所用的变换方法是.(填序号)①将菱形B向上平移;②将菱形B绕点O顺时针旋转120°;③将菱形B绕点O旋转180°.4.老师拿出6根小木棒,3根长的相同,3根短的也相同,且长的是短的的长度的2倍,请用这6根木棒摆成四个完全相同的三角形.5.为了美化绿地,要在给定的一块长方形的空地上设计一个花坛,只允许用正方形和圆两种图形,并使整个图案成轴对称,请画出两个图形.6.如图3-123所示的四个图形中,从几何图形变换的角度考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.参考答案1.B1/22.2[提示:由旋转的特征可知∠PBP′=∠ABC=90°,BP′=BP=2,在Rt△BPP′中,PP′2=BP2+BP′2=22+22=8,∴PP′=2.]3.解:(1)如图3-124所示.(2)①或③4.解:如图3-125所示.5.解:如图3-126所示.6.解:图(2),仅它不是轴对称图形.2/2