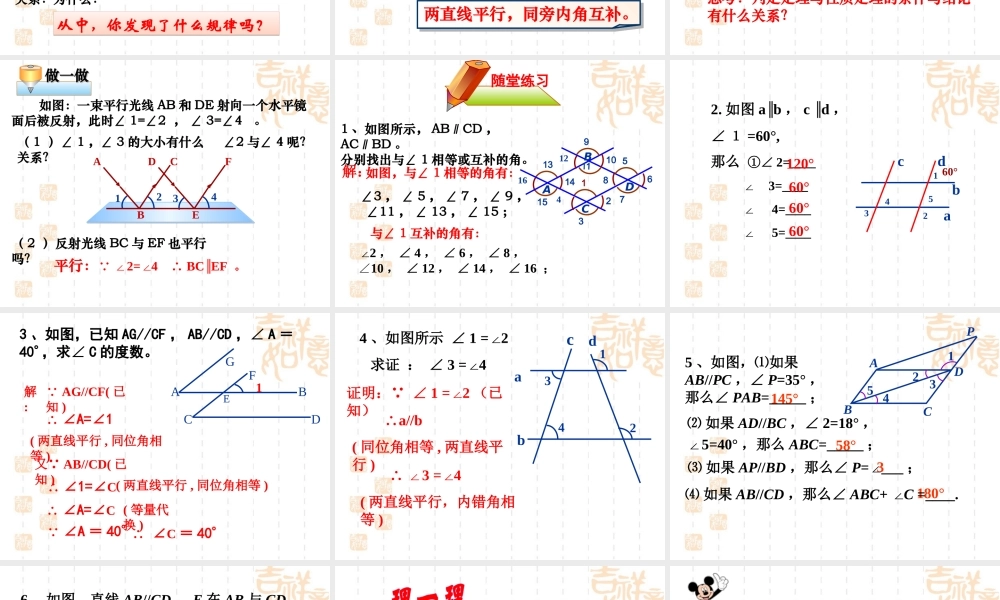
7.3平行线的性质(1)一、直线交成的角回顾&思考☞1234互补的对顶4两直线相交形成个角,从数量关系上讲,∠1与∠2形成角,从位置关系上讲,∠2与∠4形成角;对顶的两角。相等①共顶点的角:∠1与∠7形成角,∠5与∠7形成角,②不共顶点的角:F1375286DCABE4对顶互为补(1)同位角有对:∠3和∠4,4(2)内错角有对:∠5和∠4.2(3)同旁内角有对:∠5和∠22在“三线八角”中,∠1和∠2,∠5和∠6,∠7和∠8.∠7和∠4,∠7和∠2,二、判断两直线平行同位角,两直线平行.同位角,两直线平行.内错角,两直线平行.内错角,两直线平行.同旁内角,两直线平行.同旁内角,两直线平行.考察两直线是否有平行关系,我们往往用第三直线作为沟通这两直线的桥梁——考察(被第三直线截成的八个角中)不共顶点的两个角,是否满足某种数量关系.abl相等相等互补抓住被考察的两直线、寻找第三线;找出不共顶点的两个角及其数量关系,是判定两直线平行的必要途径。新知探索:二直线平行后得到什么?bac如图:直线a与b直线平行。(1)测量同位角∠1和∠5的大小,它们有什么关系?图中还有其它同位角吗?它们的大小有什么关系?(2)图中有几对内错角?它们的大小有什么关系?为什么?(3)图中有几对同旁内角?它们的大小有什么关系?为什么?从中,你发现了什么规律吗?从中,你发现了什么规律吗?83124576简记为:两条平行直线被第三条直线直线所截,两直线平行,内错角相等。两直线平行,同旁内角互补。两直线平行,同位角相等。二平行直线的特征同位角相等,内错角相等,同旁内角互补。两类定理的比较两条平行直线被第三条直线直线所截,同位角相等,两直线平行两直线平行,同位角相等。判定定理性质定理条件结论条件结论内错角相等,两直线平行两直线平行,内错角相等。同旁内角互补,两直线平行两直线平行,同旁内角互补思考:判定定理与性质定理的条件与结论有什么关系?做一做做一做如图:一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。(1)∠1,∠3的大小有什么关系?∠2与∠4呢?(2)反射光线BC与EF也平行吗? ∠2=4BCEF∠∴∥。平行:ABDECF1324随堂练习1、如图所示,AB∥CD,AC∥BD。分别找出与∠1相等或互补的角。如图,与∠1相等的角有:∠3,∠5,∠7,∠9,∠11,∠13,∠15;与∠1互补的角有:∠2,∠4,∠6,∠8,∠10,∠12,∠14,∠16;解:1141613153ABDC24567891012112.如图ab∥,cd∥,∠1=60°,那么①∠2=____∠3=____∠∠4=____∠...