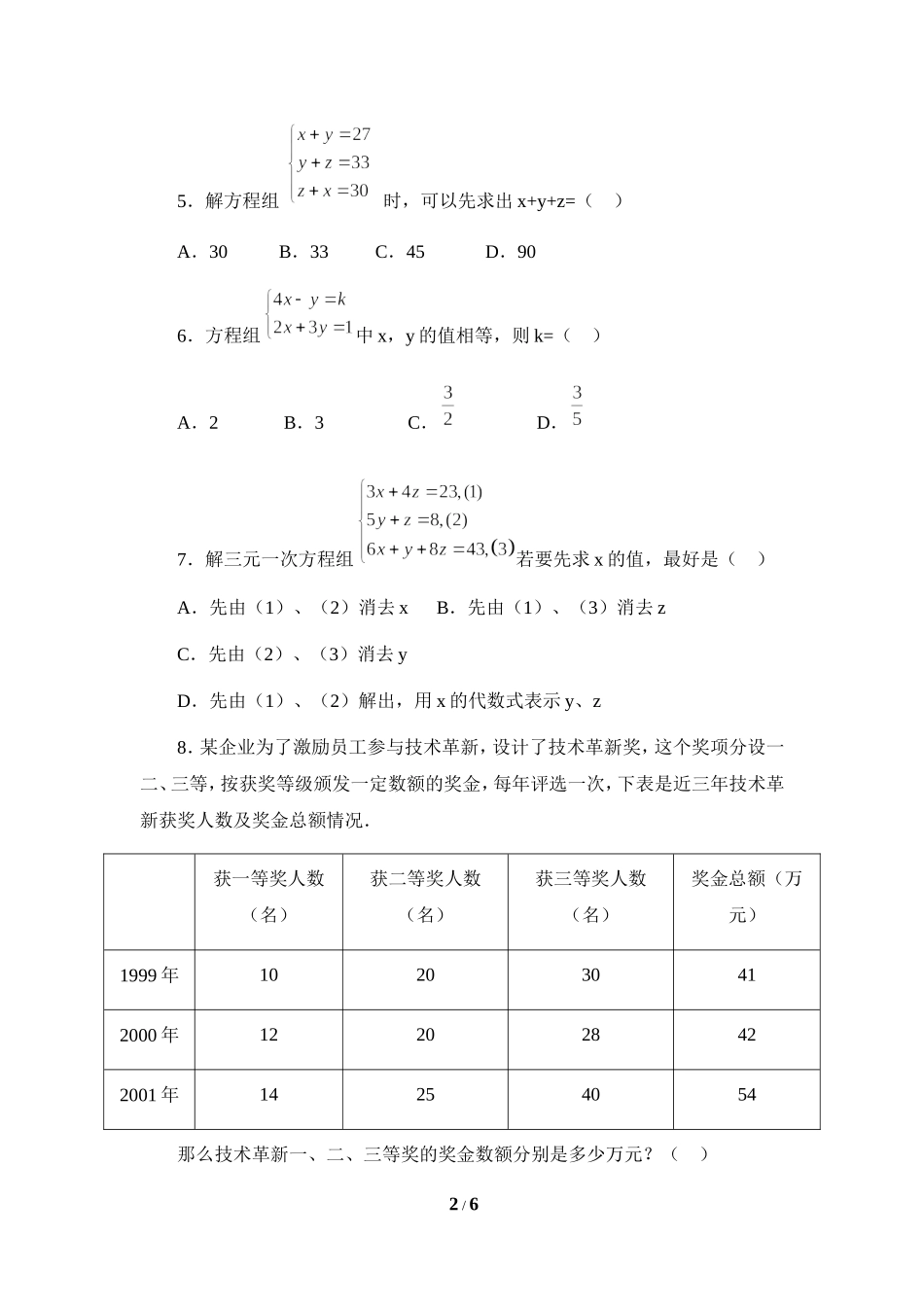
7.5三元一次方程组专项练习1.以为解建立一个三元一次方程,不正确的是()A.3x-4y+2z=3B.x-y+z=-1C.x+y-z=-2D.-y-z=12.若满足方程组的x的值是-1,y的值是1,则该方程组的解是()A.B.C.D.3.解三元一次方程组得()A.B.C.D.4.已知,则等于()A.10B.12C.14D.161/65.解方程组时,可以先求出x+y+z=()A.30B.33C.45D.906.方程组中x,y的值相等,则k=()A.2B.3C.D.7.解三元一次方程组若要先求x的值,最好是()A.先由(1)、(2)消去xB.先由(1)、(3)消去zC.先由(2)、(3)消去yD.先由(1)、(2)解出,用x的代数式表示y、z8.某企业为了激励员工参与技术革新,设计了技术革新奖,这个奖项分设一二、三等,按获奖等级颁发一定数额的奖金,每年评选一次,下表是近三年技术革新获奖人数及奖金总额情况.获一等奖人数(名)获二等奖人数(名)获三等奖人数(名)奖金总额(万元)1999年102030412000年122028422001年14254054那么技术革新一、二、三等奖的奖金数额分别是多少万元?()2/6A.一等奖4万元二等奖2.5万元三等奖0.5万元B.一等奖3.8万元二等奖2.4万元三等奖1万元C.一等奖3万元二等奖2万元三等奖1万元D.一等奖1万元二等奖0.8万元三等奖0.5万元9.用代入法解方程组得()A.B.C.D.3/6参考答案1.解:A、B、C、D四个方程都是三元一次方程,但不是方程x+y-z=-2的解.答:C2.解:x的值是-1,y的值是1,代入任意一个方程中得z=0,所以该方程组的解是答:A3.解:(1)×2-(2)得:5x+y=3(1)×3-(3)得:7x+5y=-3解方程组得x=1,y=-2把x=1,y=-2代入任意一个方程中得z=3所以方程组的解为答:B4/64.解:由已知可得=0,=0,=0解得a=1,b=-2,c=-3则等于1+4+9=14答:C5.解:把、、相加得:2x+2y+2z=90所以x+y+z=45答:C6.解:解关于x,y的方程组,即3k+1=4-2k,所以k=答:D7.解:要先求x的值,就要先消去y和z,A.B.C.的方法都不可行答:D8.解:设一、二、三等奖的奖金额分别为x万元,y万元和z万元.可得答:技术革新一、二、三等奖的奖金额分别是1万元,0.8万元和0.5万元.答:D5/69.解:由①得,y=,③把③代人②,得(能否代入①中?)3x-8()=14,所以-x=-10,x=10.(本题解完了吗?把x=10代入哪个方程求y较简单?)把x=10代入③,得y=所以y=2所以答:D6/6