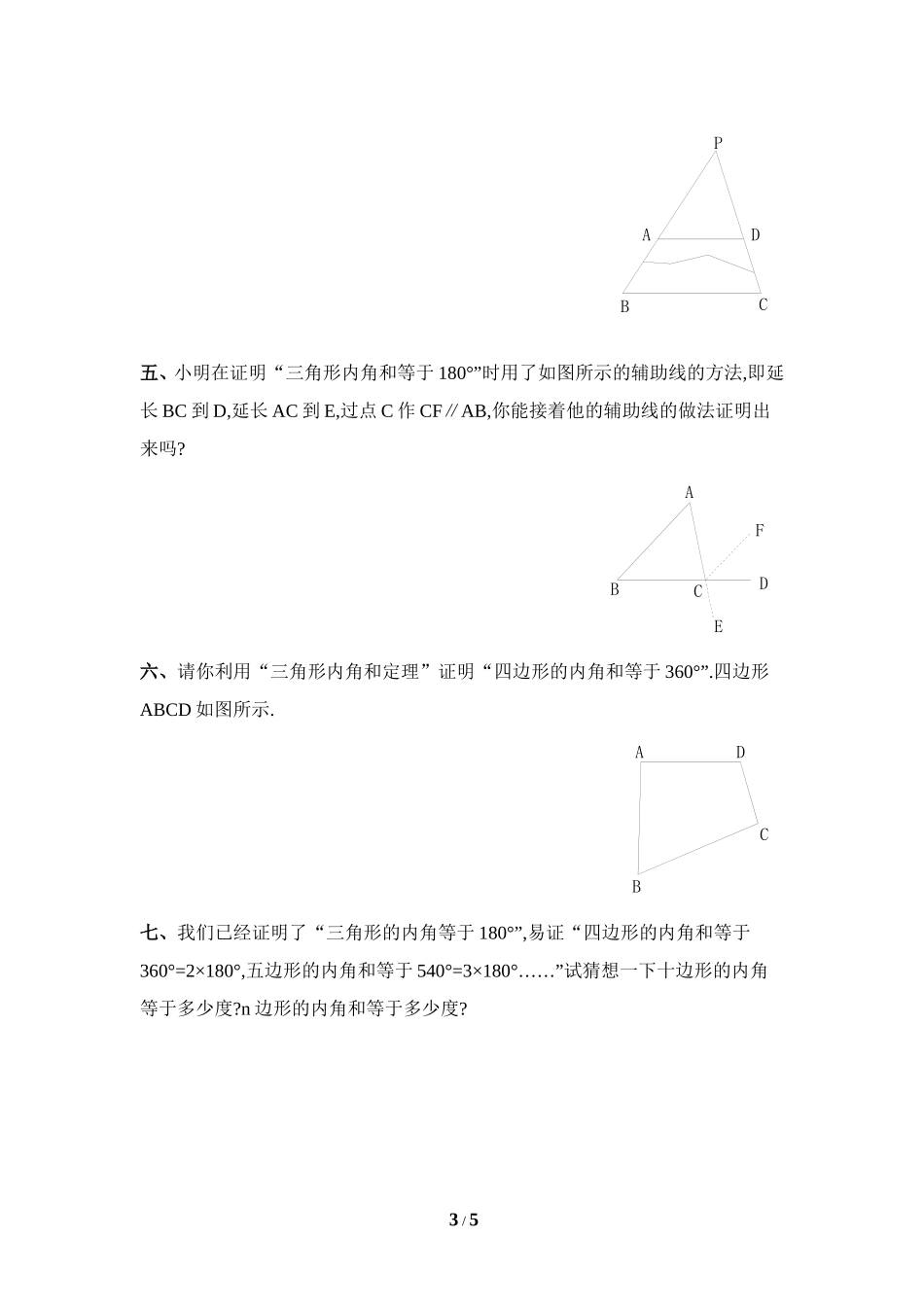
EDCBA8.6三角形内角和定理一、选择题1.如图所示,BC⊥AD,垂足是C,∠B=∠D,则∠AED与∠BED的关系是()A.∠AED>∠BEDB.∠AED<∠BEDC.∠AED=∠BEDD.无法确定2.关于三角形内角的叙述错误的是()A.三角形三个内角的和是180°B.三角形两个内角的和一定大于60°C.三角形中至少有一个角不小于60°D.一个三角形中最大的角所对的边最长3.下列叙述正确的是()A.钝角三角形的内角和大于锐角三角形的内角和B.三角形两个内角的和一定大于第三个内角C.三角形中至少有两个锐角D.三角形中至少有一个锐角.4.△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是()A.钝角三角形B.等腰直角三角形C.直角三角形D.等边三角形5.在△ABC中,∠A-∠B=35°,∠C=55°,则∠B等于()A.50°B.55°C.45°D.40°6.三角形中最大的内角一定是()A.钝角B.直角;C.大于60°的角D.大于等于60°的角二、填空题1.直角三角形的两个锐角___________.2.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是________三角形.3.在△ABC中,∠A=∠B=∠C,则∠C=_______.4.在△ABC中,A+B=120°,A-B+C=120°,∠∠∠∠∠则∠A=,1/5DCBAB=______.∠5.如图,在△ABC中,BAC=90°,ADBC∠⊥于D,则∠B=∠________,∠C=∠________.6.在一个三角形中,最多有______个钝角,至少有______个锐角.三、计算题1.如图,已知:∠A=∠C.求证:∠ADB=∠CEB.EDCBA2.如图,在△ABC中,∠B=30°,∠C=65°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.EDCBA3.如图,在正方形ABCD中,已知∠AEF=30°,∠BCF=28°,求∠EFC的度数.EFDCBA四、如图,一块梯形玻璃的下底及两腰的一部分被摔碎,量得∠A=120°,∠D=105°,你能否求出两腰的夹角∠P的度数.2/5PDCBA五、小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的做法证明出来吗?EFDCBA六、请你利用“三角形内角和定理”证明“四边形的内角和等于360°”.四边形ABCD如图所示.DCBA七、我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180°……”试猜想一下十边形的内角等于多少度?n边形的内角和等于多少度?3/5参考答案一、1.C2.B3.C4.D5.C6.D二、1.互余2.直角3.150°4.90°,30°5.∠DAC;∠BAD6.1;2三、1. ∠A+∠B+∠ADB=∠C+∠B+∠CEB又 ∠A=∠C,∠B=∠B∴∠ADB=∠CEB2. ∠B+∠C+∠BAC=180°∴∠BAC=180°-∠B-∠C=180°-30°-66°=84°又 AD平分∠BAC∴∠DAC=∠BAC=×84°=42° AE⊥BC...