3.1.1 同底数幂的乘法（1）.pptxVIP免费

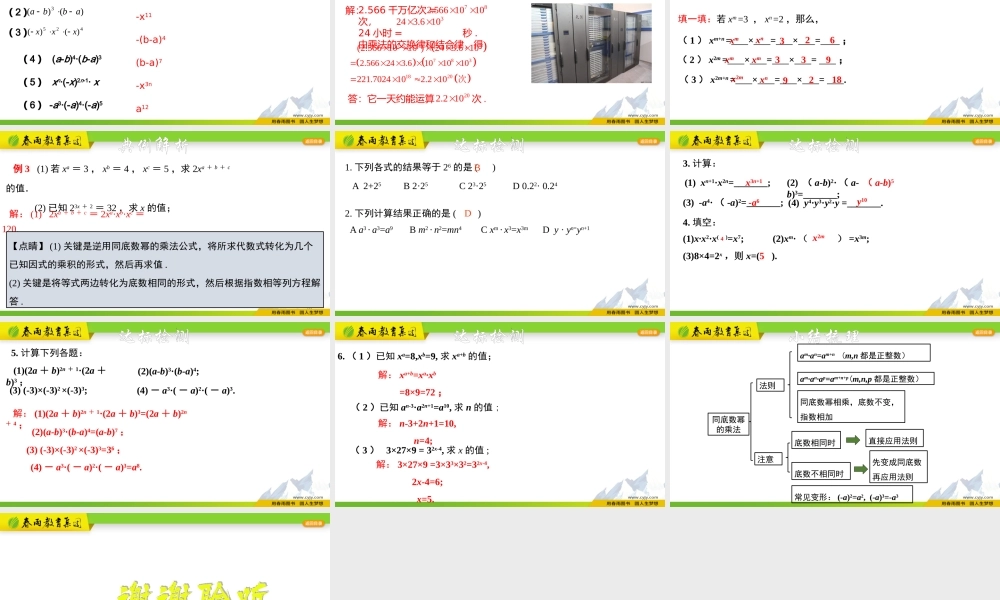
学习目标理解并掌握同底数幂的乘法法则.能够运用同底数幂的乘法法则进行相关计算.光年是长度单位，1光年指光经过一年所行的距离.光的速度大约是3km/s，若1年以365天计，则1光年大约是多少千米？(一年相当于秒）510知识精讲问题1怎样列式？(3×105)×(3×107)问题2在105中，10，5分别叫什么？表示的意义是什么？=10×10×105个10相乘105底数幂指数问题3观察算式105×107，两个因式有何特点？观察可以发现，105和107这两个因数底数相同，是同底数的幂的形式.我们把形如105×107这种运算叫作同底数幂的乘法.知识精讲3×3×107=3×3×105×107=9×1012答：1光年大约是9×1012千米.510问题4根据乘方的意义，想一想如何求1光年大约是多少千米？知识精讲根据幂的意义，以及有理数的乘法，请完成下列问题：（1）是多少个2相乘？232222222222322（2）（）（）621010=1010（3）（）（）34aa=aa2222253210101010101010101010101010101010826aaaaaaaaaaaaaa743知识精讲对于上述计算，你发现同底数幂相乘有什么规律吗？可以大胆猜想.猜想:am·an=?(当m、n都是正整数)am+n分组讨论，并尝试证明你的猜想是否正确.知识精讲猜想:am·an=(当m、n都是正整数)am·an=m个an个a=aa…a=am+n(m+n)个a即:am·an=am+n(当m、n都是正整数)（aa…a）（aa…a）am+n（乘方的意义）（乘法结合律）（乘方的意义）验证：知识精讲am·an=am+n(m、n都是正整数).同底数幂相乘,底数，指数.不变相加.同底数幂的乘法法则：结果：①底数不变②指数相加条件：①乘法②底数相同知识精讲思考：当三个或三个以上同底数幂相乘时，同底数幂的乘法公式是否也适用呢？怎样用公式表示？am·an·ap=（m、n、p都是正整数）am+n+p例1计算下列各式，结果用幂的形式表示.（6）(a-b)2·(a-b)3（1）（2）（3）（4）（5）3877782266453xx5233117152568x735ab典例解析运用同底数幂的乘法法则计算下列各式425)()(xxx)()(3abba(1)(-8)5×82（4）(a-b)4·(b-a)3（5）xn·(-x)2n-1·x（6）-a3·(-a)4·(-a)5（2）（3）-87-x11-(b-a)4(b-a)7-x3na12针对练习例2：“我国天河-1A”超级计算机的实测运算速度达到每秒2.566千万亿次.如果按这个速度工作一整天，那么它能运算多少次？2.566千万亿次=次，2...