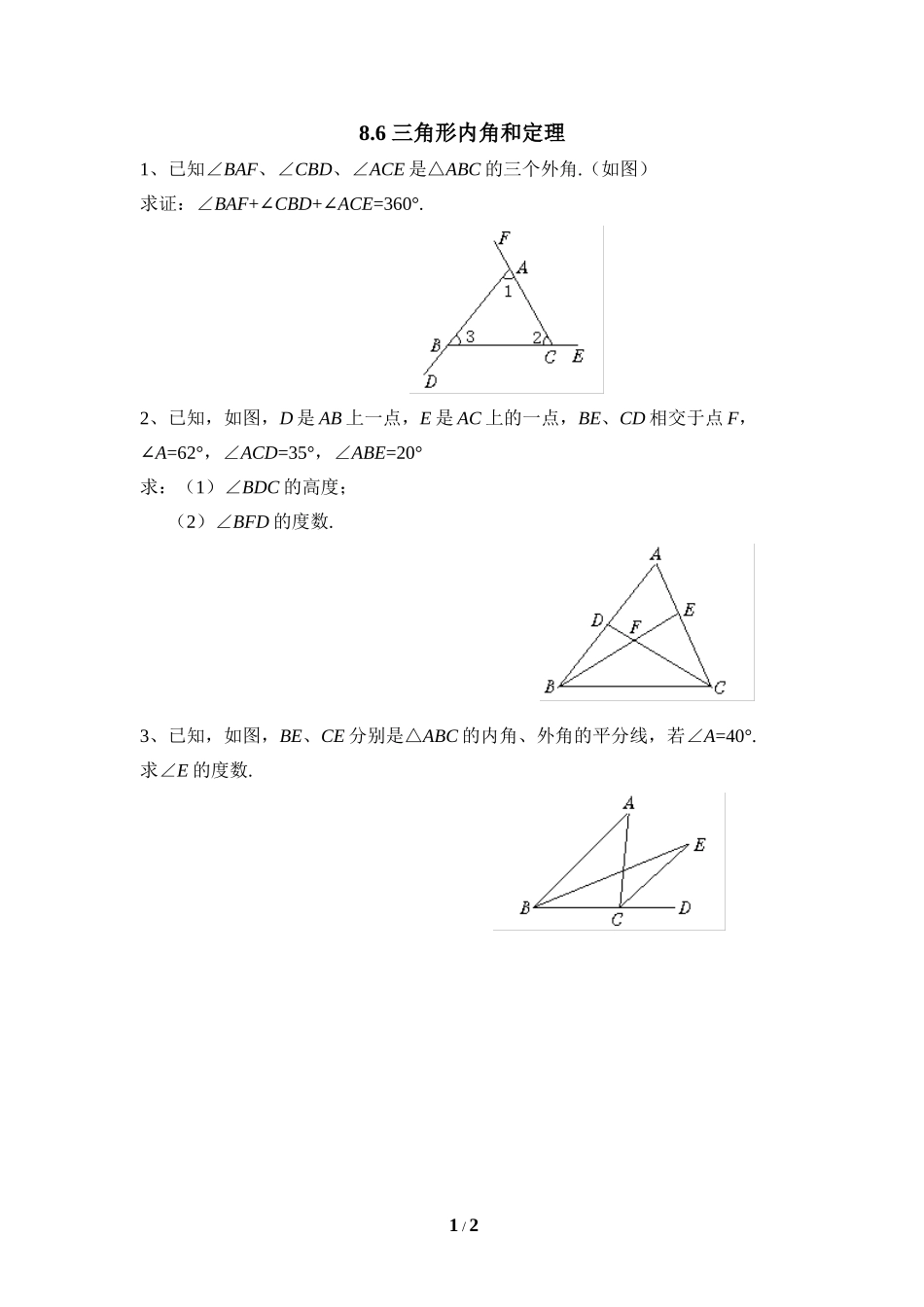
8.6三角形内角和定理1、已知∠BAF、∠CBD、∠ACE是△ABC的三个外角.(如图)求证:∠BAF+∠CBD+∠ACE=360°.2、已知,如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°求:(1)∠BDC的高度;(2)∠BFD的度数.3、已知,如图,BE、CE分别是△ABC的内角、外角的平分线,若∠A=40°.求∠E的度数.1/2参考答案1、证明:∵∠BAF、∠CBD、∠ACE是△ABC的三个外角.(已知)∴∠BAF=2+3.∠∠∠CBD=1+2∠∠∠ACE=1+3∠∠(三角形的一个外角等于和它不相邻的两个内角的和)∴∠BAF+∠CBD+∠ACE=2(∠1+2+3∠∠)(等式的性质)1+2+3=180°∠∠∠(三角形的内角和定理)∴∠BAF+∠CBD+∠ACE=2×180°=360°(等量代换)2、解:∵∠BDC=∠A+∠ACD(三角形的一个外角等于和它不相邻的两个内角的和)∠A=62°∠ACD=35°∴∠BDC=62°+35°=97°(等量代换)(2)∵∠BFD+∠BDC+∠ABE=180°(三角形内角和定理)∴∠BFD=180°-∠BDC-∠ABE(等式的性质)∵∠BDC=97°∠ABE=20°(已知)∴∠BFD=180°-97°-20°=63°(等量代换)3、解:∵∠ECD是△BCE的外角(已知)∴∠ECD=∠EBC+∠E(三角形的一个外角等于和它不相邻的两个内角的和)∵BE、CE分别平分∠ABC、∠ACD(已知)∴∠EBC=∠ABC,∠ECD=∠ACD(角平分线的定义)∴∠ACD=∠ABC+∠E(等量代换)∴∠ACD=∠ABC+2∠E(等式的性质)又∵∠ACD是△ABC的外角(已知)∴∠ACD=∠A+∠ABC(三角形的一个外角等于和它不相邻的两个内角的和)∴∠A+∠ABC=∠ABC+2∠E(等量代换)∴∠A=2∠E(等式的性质)∴∠E=∠A=×40°=20°(等式的性质)2/2