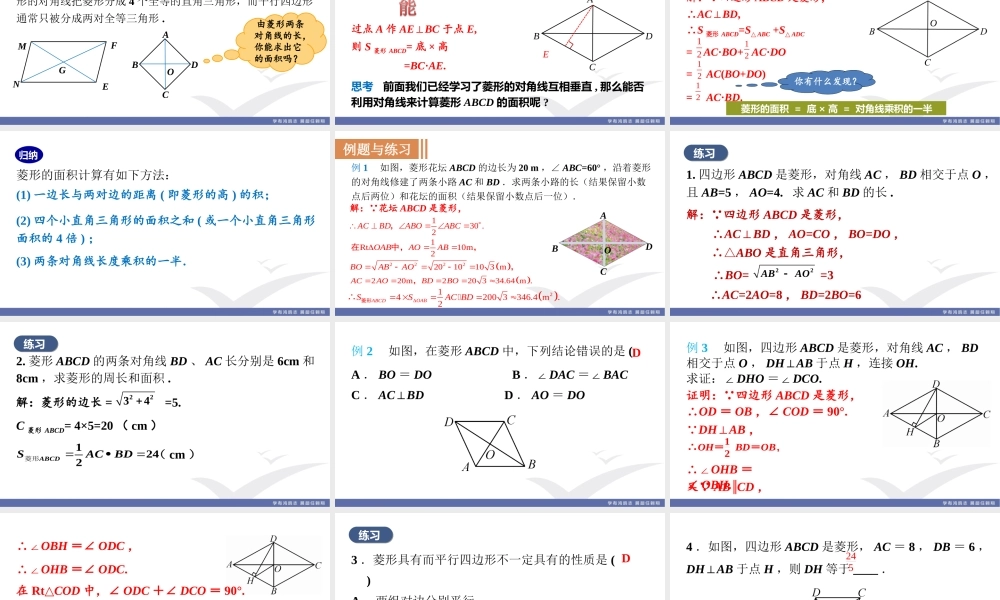
第十八章平行四边形18.2特殊的平行四边形18.2.1菱形第1课时菱形的性质导入新课欣赏下面图片,图片中框出的图形是你熟悉的吗?将一张矩形的纸对折,然后沿着图中的虚线剪下,猜猜看,打开是个什么图形,自己动手做一做.观察得到的四边形的形状,它是一个怎样的四边形呢?思考探究新知平行四边形矩形前面我们学习了平行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.有一个角是直角思考如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?平行四边形菱形邻边相等定义:菱形是特殊的平行四边形.平行四边形不一定是菱形.归纳有一组邻边相等的平行四边形.探究新知活动在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:问题1菱形是轴对称图形吗?如果是,指出它的对称轴.是,两条对角线所在直线都是它的对称轴.问题1根据上面折叠过程,猜想菱形的四边在数量上有什么关系?菱形的两条对角线有什么关系?猜想猜想11菱形的四条边都相菱形的四条边都相等等..猜想猜想22菱形的两条对角线互相垂菱形的两条对角线互相垂直,并且每一条对角线平分一组直,并且每一条对角线平分一组对角对角..已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.证明:(1) 四边形ABCD是平行四边形,ABCOD证一证求证:(1)AB=BC=CD=AD;(2)AC⊥BD;∠DAC=∠BAC,∠DCA=∠BCA,∠ADB=∠CDB,∠ABD=∠CBD.∴AB=CD,AD=BC(平行四边形的对边相等).又 AB=AD,∴AB=BC=CD=AD.解:(2) AB=AD,ABCOD∴△ABD是等腰三角形.又 四边形ABCD是平行四边形,∴OB=OD(平行四边形的对角线互相平分).在等腰三角形ABD中, OB=OD,∴AO⊥BD,AO平分∠BAD,即AC⊥BD,∠DAC=∠BAC.同理可证∠DCA=∠BCA,∠ADB=∠CDB,∠ABD=∠CBD.知识归纳对边相等四个角都是直角对角线互相平分且相等四边相等对角相等两条对角线互相垂直平分,并且每一条对角线平分一组对角矩形的性质菱形的性质对角相等对角线互相平分对边相等平行四边形的性质比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.探究新知由菱形两条对角线的长,你能求出它的面积吗?FMNEGABDCO问题2菱形是特殊的平行四边形,那么能否利用平行四边形的面积公式计算菱形ABCD的面积呢?ABCD思考前面我们已经学...