4.6一元二次方程根与系数的关系.pptxVIP免费

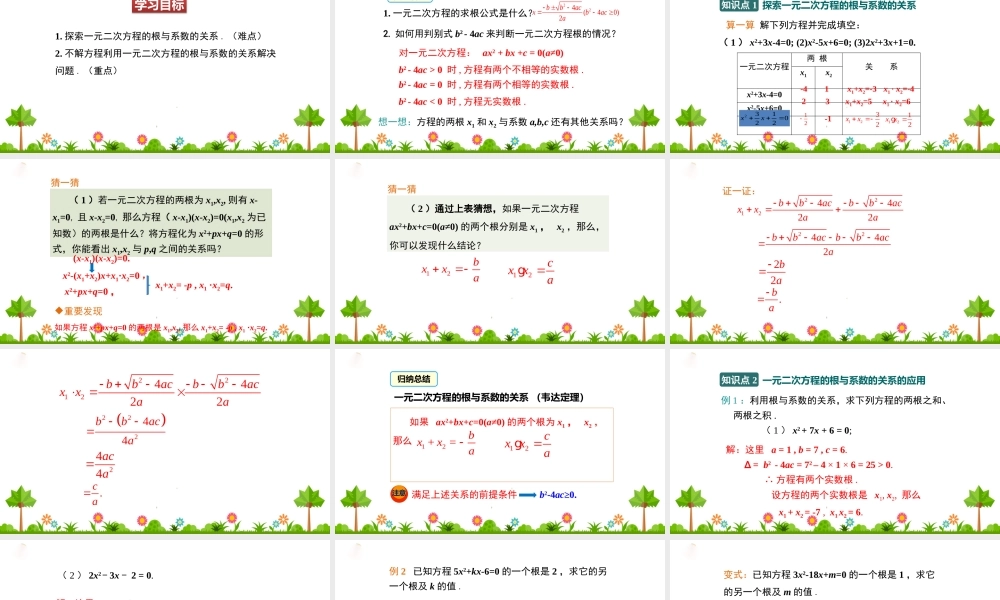
4.6一元二次方程根与系数的关系1.探索一元二次方程的根与系数的关系.（难点）2.不解方程利用一元二次方程的根与系数的关系解决问题.（重点）学习目标复习引入1.一元二次方程的求根公式是什么？224(40)2bbacxbaca想一想：方程的两根x1和x2与系数a,b,c还有其他关系吗？2.如何用判别式b2-4ac来判断一元二次方程根的情况？对一元二次方程：ax2+bx+c=0(a≠0)b2-4ac>0时,方程有两个不相等的实数根.b2-4ac=0时,方程有两个相等的实数根.b2-4ac<0时,方程无实数根.导入新课算一算解下列方程并完成填空：（1）x2+3x-4=0;(2)x2-5x+6=0;(3)2x2+3x+1=0.一元二次方程两根关系x1x2x2+3x-4=0x2-5x+6=02x2+3x+1=0-412312-1x1+x2=-3x1·x2=-4x1+x2=5x1·x2=6231022xx1232xx1212xxg讲授新课探索一元二次方程的根与系数的关系知识点1知识点1猜一猜（1）若一元二次方程的两根为x1,x2,则有x-x1=0,且x-x2=0,那么方程（x-x1)(x-x2)=0(x1,x2为已知数）的两根是什么？将方程化为x2+px+q=0的形式，你能看出x1,x2与p,q之间的关系吗？重要发现如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=-p,x1·x2=q.(x-x1)(x-x2)=0.x2-(x1+x2)x+x1·x2=0，x2+px+q=0，x1+x2=-p,x1·x2=q.猜一猜（2）通过上表猜想，如果一元二次方程ax2+bx+c=0(a≠0)的两个根分别是x1，x2，那么，你可以发现什么结论？12bxxa12cxxag22124422bbacbbacxxaa22442bbacbbaca22ba.ba证一证：22124422bbacbbacxxaa22244bbaca244aca.ca一元二次方程的根与系数的关系（韦达定理）如果ax2+bx+c=0(a≠0)的两个根为x1，x2，那么12bx+x=a12cxxag注意满足上述关系的前提条件b2-4ac≥0.归纳总结例1：利用根与系数的关系，求下列方程的两根之和、两根之积.（1）x2+7x+6=0;解：这里a=1,b=7,c=6.Δ=b2-4ac=72–4×1×6=25>0.∴方程有两个实数根.设方程的两个实数根是x1,x2,那么x1+x2=-7,x1x2=6.一元二次方程的根与系数的关系的应用知识点2知识点2（2）2x2-3x-2=0.解：这里a=2,b=-3,c=-2.Δ=b2-4ac=（-3）2–4×2×(-2)=25>0,∴方程有两个实数根.设方程的两个实数根是x1,x2,那么x1+x2=,x1x2=-1.32例2已知方程5x2+kx-6=0的一个根是2，求它的另一个根及k的值.解：设方程的两个根分别是x1、x2，其中x1=2.所以：x1·x2=2x2=即：x2=由于x1+x2=2+=得：k=－7.答：方程的另一个根是，k=－7.,5k3.53()5356,5变式...