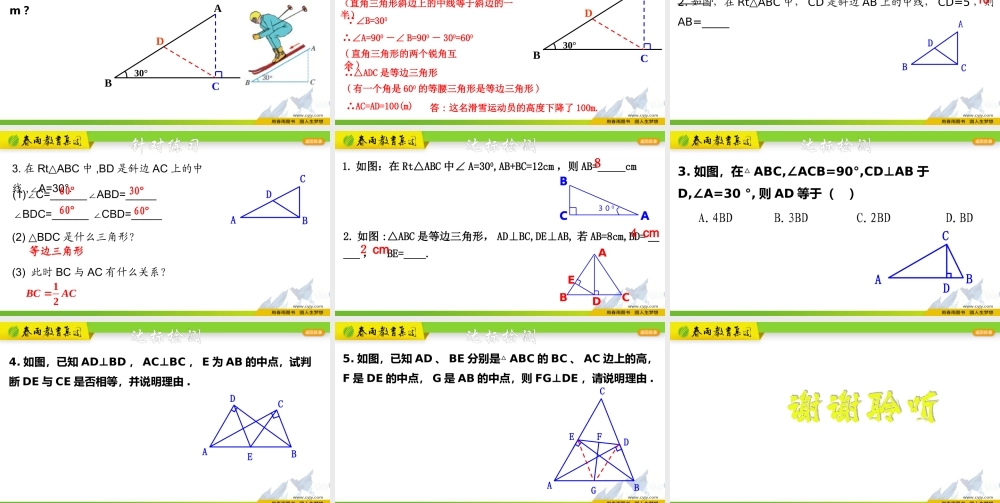
有一个角是直角的三角形叫做直角三角形.直角三角形表示:Rt△直角边ABC斜边直角边直角三角形ABC表示为Rt△ABC,∠ACB为Rt∠.直角三角形的定义知识精讲直角三角形的性质一直角三角形的两个锐角互余.ABC ∠ACB=90°()∴∠A+∠B=90°几何语言:在△ABC中()直角三角形的两个锐角互余已知知识精讲1.△在ABC中,∠C=90°,∠A=30°,∠B=.2.直角三角形两个锐角之差是10°,则较大的锐角是____度.3.直角三角形的两个锐角的平分线所构成的角是度.60°50°45°或135°4.一个三角形的三个内角之比是1:2:3,则这个三角形是______三角形.直角针对练习FBDECA5.如图,由一副三角尺组成的图案,则∠DCF=_____,∠CFD=_____,∠AEF=______6007501350针对练习例1:如图,CD是Rt△ABC斜边上的高.典例解析CBD12(1)图中有几个直角三角形?Rt△ABC、Rt△ACD、Rt△BCD(2)图中有几对互余的角?∠A与∠B、∠A与∠1、∠1与∠2、∠B与∠2(3)图中有几对相等的角?∠1=∠B、∠2=∠AABC等腰直角三角形的两个锐角为_____度.45°两条直角边相等的直角三角形叫做等腰直角三角形.等腰直角三角形知识精讲例2:如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD.请说明理由.ABDC典例解析证明: △ABC为等腰直角三角形∴∠B=∠C=45°,∠BAC=90°,AB=AC AD是斜边BC上的高∴∠ADB=∠ADC=90°,∠BAD=∠CAD=45°∴∠B=∠C=∠BAD=∠CAD∴AD=BD=CD.DCBAE证明:延长CD至E,使DE=CD,连结BE. CD是Rt△ABC斜边AB上的中线∴AD=BD ∠ADC=∠BDE∴△ADC≌△BDE(SAS)∴AC=BE,∠ACD=∠BED∴AC∥BE∴∠ACB+∠CBE=180°知识精讲直角三角形斜边上的中线等于斜边的一半.DCBA ∠ACB=900,CD是AB边上的中线∴CD=AB21几何语言:直角三角形的性质二知识精讲例3一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B.已知AB=200m,问这名滑雪运动员的高度下降了多少m?30°ACBD典例解析解:如图,作Rt△ABC的斜边上的中线CD,则CD=AD=0.5AB=0.5×200=100m(直角三角形斜边上的中线等于斜边的一半) ∠B=300∴∠A=900-∠B=900-300=600(直角三角形的两个锐角互余)∴△ADC是等边三角形(有一个角是600的等腰三角形是等边三角形)∴AC=AD=100(m)答:这名滑雪运动员的高度下降了100m.30°ACBD典例解析1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.2.如图,在Rt△ABC中,CD是斜边AB上的中线,CD=5,则AB=_____CBD5cm10针对练习3.在RtABC△中,BD是斜边AC上的中线,A=30°.∠ABCD(1)C=___...