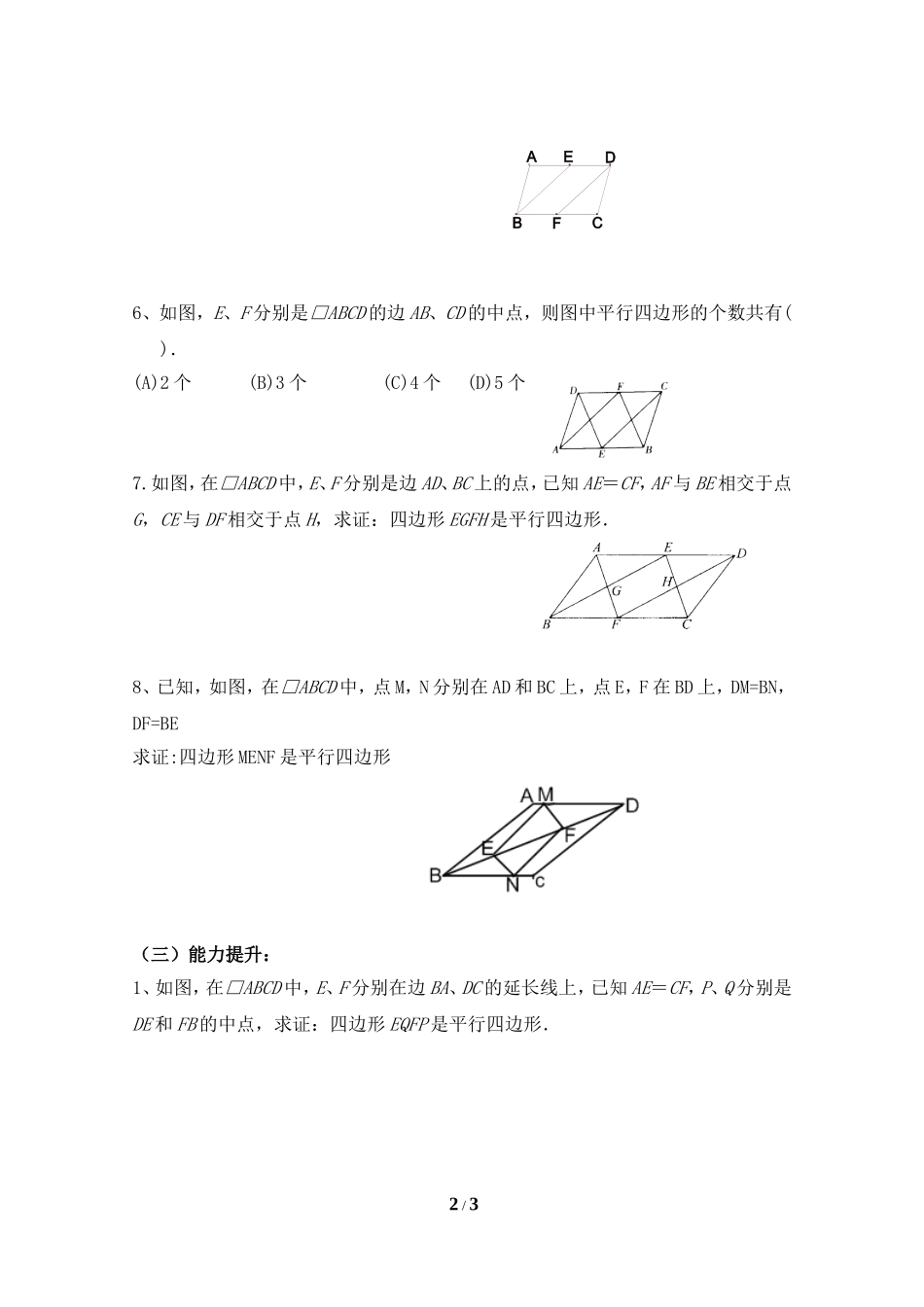
课题5.2平行四边形的判定第二课时学习几何,增强我们的理性思维。学习目标1、经历平行四边形判定定理的探索过程,发展推理能力.2、探索并证明平行四边形的判定定理及其他相关结论,发展演绎推理能力。3、体会归纳、类比、转化等数学思想。重点难点重点:理解平面四边形判定定理的探究过程难点:平面四边形判定定理的应用学习方法小组合作,共同探究学习流程:(一)复习回顾:我们已经学过的平行四边形的判定方法有哪些?(二)探究新知合作探究一:取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?(即“一组对边平行且相等的四边形是平行四边形”吗?)1、已知:求证:证明:2、归纳:的四边形是平行四边形3、几何语言表述:∵∴四边形ABCD是平行四边形.4、能判定四边形ABCD是平行四边形的题设是().(A)AD=BC,AB∥CD(B)∠A=∠B,∠C=∠D(C)AB=BC,AD=DC(D)AB∥CD,CD=AB5、已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF1/3你有几种证明方法?6、如图,E、F分别是□ABCD的边AB、CD的中点,则图中平行四边形的个数共有().(A)2个(B)3个(C)4个(D)5个7.如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.8、已知,如图,在□ABCD中,点M,N分别在AD和BC上,点E,F在BD上,DM=BN,DF=BE求证:四边形MENF是平行四边形(三)能力提升:1、如图,在□ABCD中,E、F分别在边BA、DC的延长线上,已知AE=CF,P、Q分别是DE和FB的中点,求证:四边形EQFP是平行四边形.2/3FEABDC2、在四边形ABCD中,AD=BC,当∠A与∠B满足的关系时,四边形ABCD是平行四边形(四)课堂练习:课本131页随堂练习1、2、习题5.51A类课本132页习题5.53、4、B类(五)课堂小结:我的收获:我的疑惑:3/3