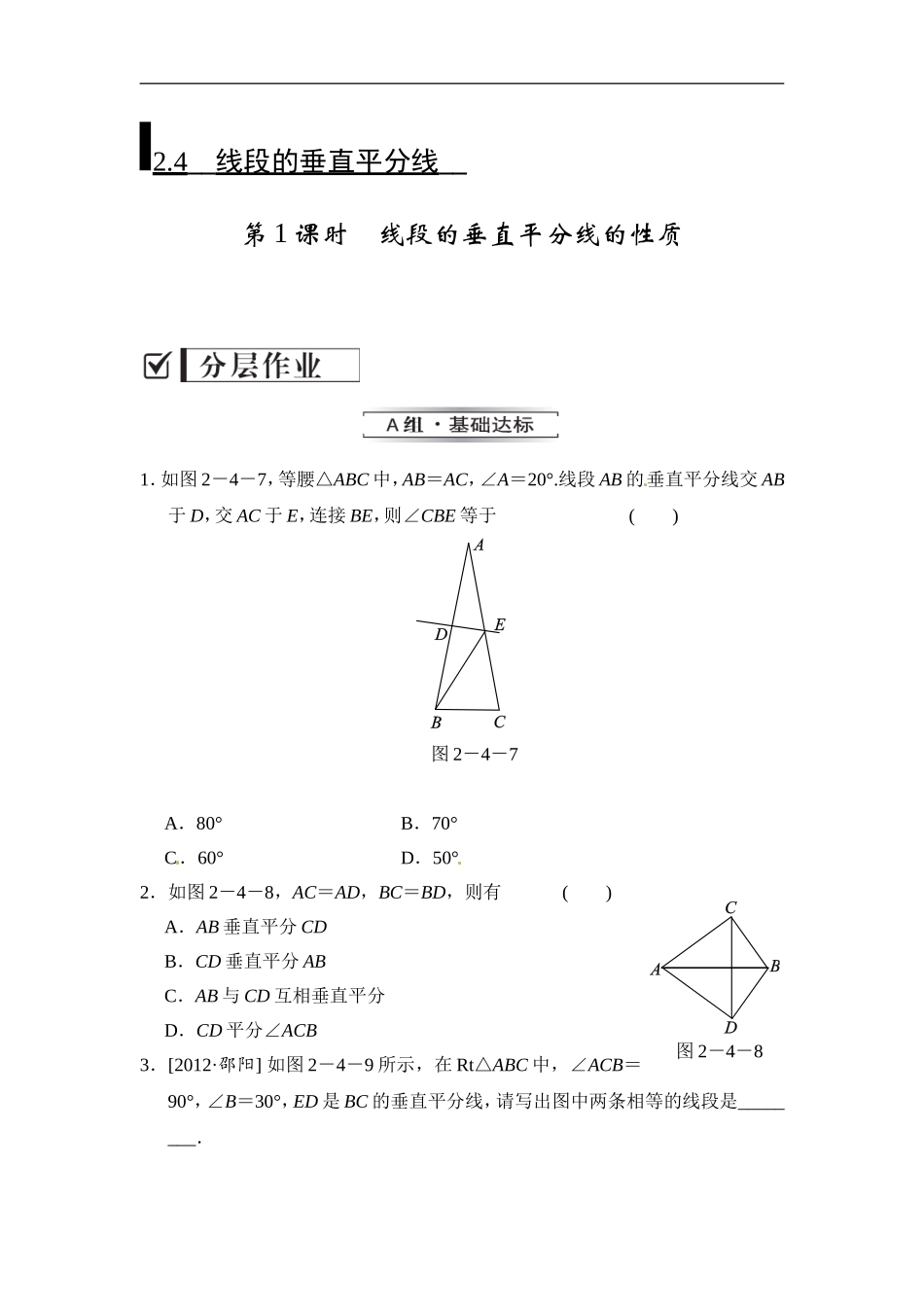
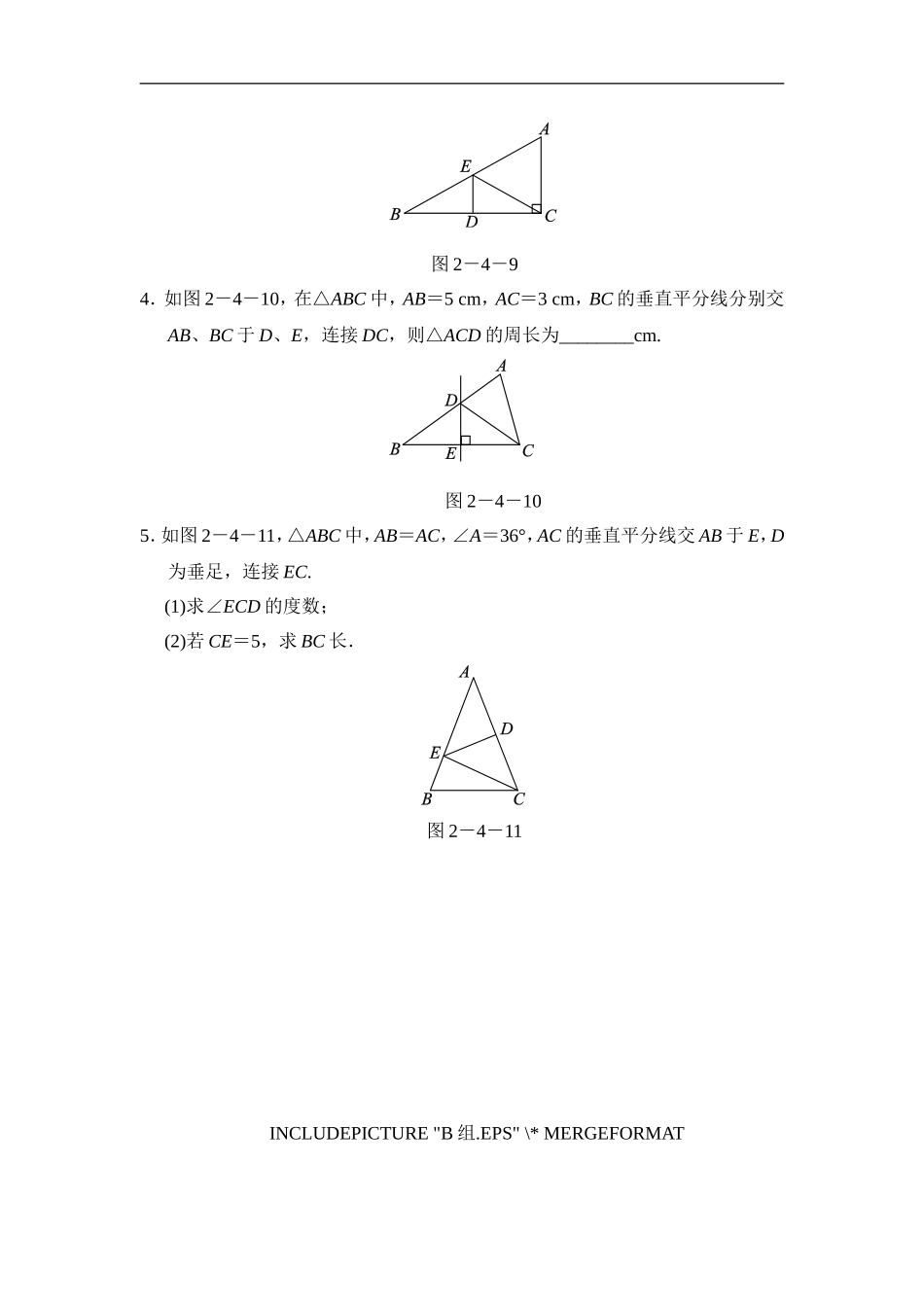
2.4__线段的垂直平分线__第1课时线段的垂直平分线的性质1.如图2-4-7,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()图2-4-7A.80°B.70°C.60°D.50°2.如图2-4-8,AC=AD,BC=BD,则有()A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB3.[2012·邵阳]如图2-4-9所示,在Rt△ABC中,∠ACB=90°,∠B=30°,ED是BC的垂直平分线,请写出图中两条相等的线段是________.图2-4-8图2-4-94.如图2-4-10,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,连接DC,则△ACD的周长为________cm.图2-4-105.如图2-4-11,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.图2-4-11[来源:Zxxk.Com]INCLUDEPICTURE"B组.EPS"\*MERGEFORMAT6.如图2-4-12,△ABC中,边AB、BC的垂直平分线交于点P.(1)求证:PA=PB=PC.(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?图2-4-12[来源:学科网]INCLUDEPICTURE"C组.EPS"\*MERGEFORMAT7.根据图2-4-13,解答下列各题.(1)在△ABC中,AB=AC,∠BAC=100°,ME和NF分别垂直平分AB和AC,求∠MAN的度数.(2)在(1)中,若无AB=AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.(3)在(2)的情况下,若BC=10cm,试求出△AMN的周长.图2-4-13答案解析1.C【解析】因为等腰△ABC中,AB=AC,∠A=20°,所以∠ABC==80°.[来源:Z。xx。k.Com]因为DE是线段AB的垂直平分线,所以AE=BE,∠A=∠ABE=20°,所以∠CBE=∠ABC-∠ABE=80°-20°=60°.故选C.2.A【解析】因为AC=AD,BC=BD,所以点A,B在线段CD的垂直平分线上.所以AB垂直平分CD.故选A.3.BD=CD(答案不唯一)【解析】因为ED是BC的垂直平分线,所以BE=CE,BD=CD,因为在Rt△ABC中,∠ACB=90°,∠B=30°,所以∠ECB=∠B=30°,∠A=90°-∠B=60°,所以∠ACE=90°-30°=60°,所以△AEC是等边三角形,所以AE=EC=AC,所以AE=AC=EC=BE.所以图中两条相等的线段是:BE=CE=AC=AE或BD=CD.故答案为:此题答案不唯一,如BD=CD等.4.8【解析】因为DE为BC的垂直平分线,所以CD=BD,所以△ACD的周长为AC+CD+AD=AC+AD+BD=AC+AB,又因为AC=3cm,AB=5cm,所以△ACD的周长为3+5=8(cm).5.解:(1)因为DE垂直平分AC,所...