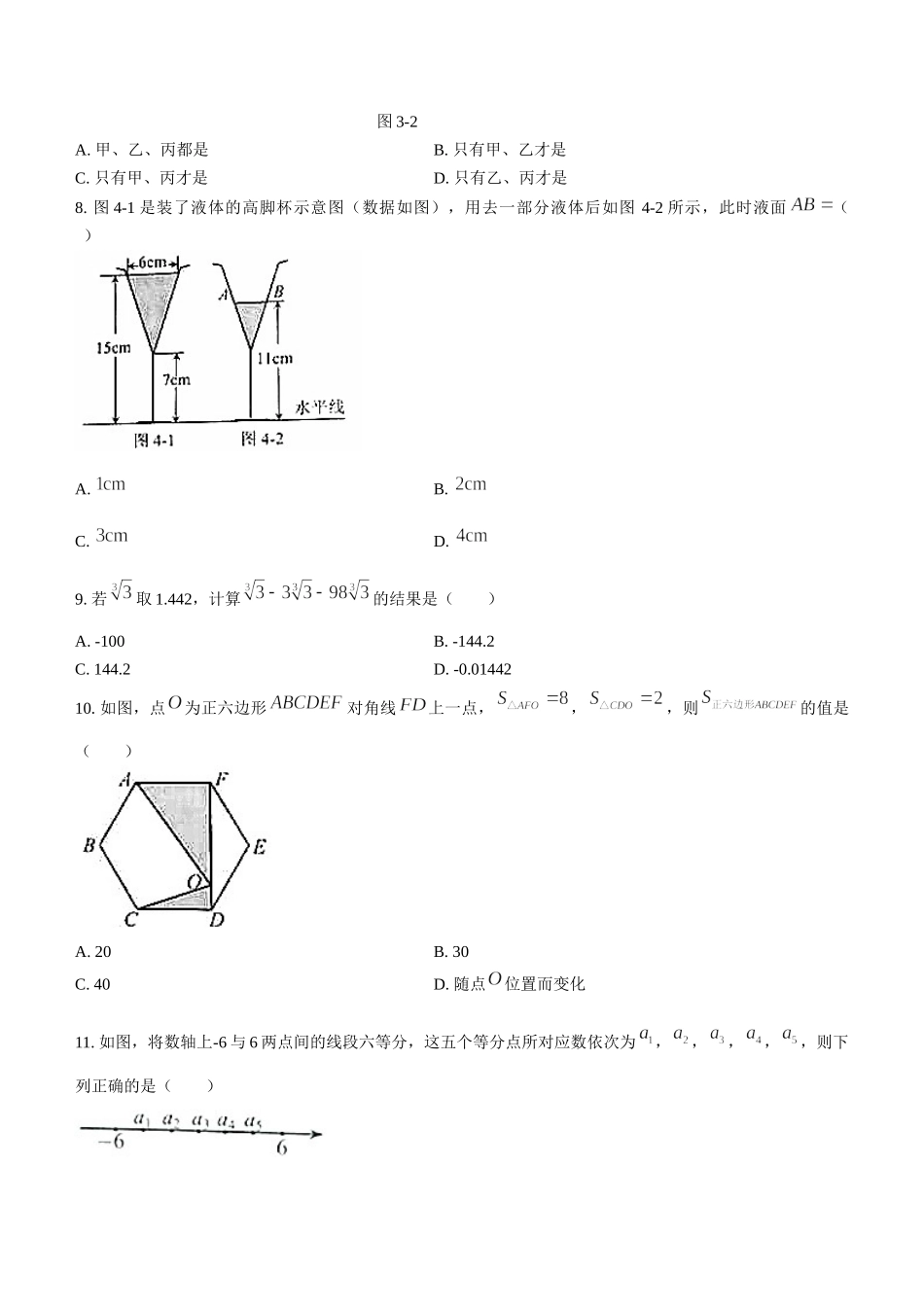
2021年河北省初中毕业生升学文化课考试数学试卷注意事项:1.本试卷共8页,总分120分,考试时间120分钟.2.答题前,考生务必将姓名、准考证号填写在试卷和答题卡相应位置上.3.答选择题时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,将答案写在答题卡上.写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,已知四条线段,,,中的一条与挡板另一侧的线段在同一直线上,请借助直尺判断该线段是()A.B.C.D.2.不一定相等的一组是()A.与B.与C.与D.与3.已知,则一定有,“”中应填的符号是()A.B.C.D.4.与结果相同的是()A.B.C.D.5.能与相加得0的是()A.B.C.D.6.一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是()A.代表B.代表C.代表D.代表7.如图3-1,中,,为锐角.要在对角线上找点,,使四边形为平行四边形,现有图3-2中的甲、乙、丙三种方案,则正确的方案()取中点,作,作于于作,分别平分,图3-2A.甲、乙、丙都是B.只有甲、乙才是C.只有甲、丙才是D.只有乙、丙才是8.图4-1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图4-2所示,此时液面()A.B.C.D.9.若取1.442,计算的结果是()A.-100B.-144.2C.144.2D.-0.0144210.如图,点为正六边形对角线上一点,,,则的值是()A.20B.30C.40D.随点位置而变化11.如图,将数轴上-6与6两点间的线段六等分,这五个等分点所对应数依次为,,,,,则下列正确的是()A.B.C.D.12.如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是()A.0B.5C.6D.713.定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,是的外角。求证:.证法1:如图, (三角形内角和定理),又 (平角定义),∴(等量代换).∴(等式性质).证法2:如图, ,,且(量角器测量所得),又 (计算所得),∴(等量代换).下列说法正确的是()A.证法1还需证明其他形状的三角形,该定理的证明才完整B.证法1用严谨的推理证明了该定理C.证法2用特殊到一般法证明了该定理D.证法2只要测量够一百个三角形进行验证,就能证明该定理14.小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图9-1及条形图9-2(柱的高度从高到低排列).条形图不小心被撕了...