26.1.2（4） 比例系数k的几何意义.pptVIP免费

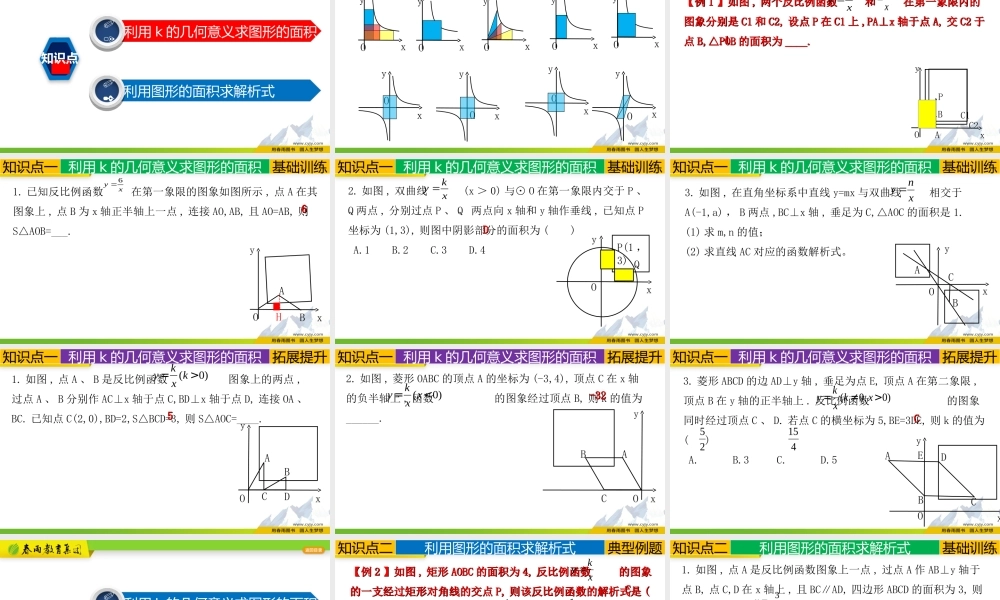
26.1.2(4)反比例函数的图象和性质探究新知知识归纳典型例题当堂训练课堂小结导入新课---比例系数k的几何意义利用k的几何意义求图形的面积01利用图形的面积求解析式02知识点yOxyOxyOxyOxyOxyOxyOxyOxyOx要点归纳知识点一利用k的几何意义求图形的面积【例【例11】如图】如图,,两个反比例函数和在第一象限内的两个反比例函数和在第一象限内的图象分别是图象分别是C1C1和和C2,C2,设点设点PP在在C1C1上上,PA⊥x,PA⊥x轴于点轴于点A,A,交交C2C2于于点点B,△POBB,△POB的面积为的面积为____.____.xy4xy2xPyOABC1C211典型例题知识点一利用k的几何意义求图形的面积1.已知反比例函数在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO,AB,且AO=AB,则S△AOB=___.xy6xAyOB66H基础训练知识点一利用k的几何意义求图形的面积2.如图,双曲线(x＞0)与⊙O在第一象限内交于P、Q两点,分别过点P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为()A.1B.2C.3D.4xkyDDxP(1，3)yOQ基础训练知识点一利用k的几何意义求图形的面积3.如图,在直角坐标系中直线y=mx与双曲线相交于A(-1,a)，B两点,BC⊥x轴,垂足为C,△AOC的面积是1.(1)求m,n的值；(2)求直线AC对应的函数解析式。xnyyOxABC基础训练知识点一利用k的几何意义求图形的面积1.如图,点A、B是反比例函数图象上的两点,过点A、B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA、BC.已知点C(2,0),BD=2,S△BCD=3,则S△AOC=____.)0(>=kxky55yOxABDC拓展提升知识点一利用k的几何意义求图形的面积2.如图,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数的图象经过顶点B,则k的值为______.)0(<=xxky-32-32yOxACB拓展提升知识点一利用k的几何意义求图形的面积yOxACBDE3.菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上.反比例函数的图象同时经过顶点C、D.若点C的横坐标为5,BE=3DE,则k的值为()A.B.3C.D.5)0,0(>≠=xkxky25415CC拓展提升知识点一利用k的几何意义求图形的面积利用k的几何意义求图形的面积01利用图形的面积求解析式02知识点CC【例【例22】如图】如图,,矩形矩形AOBCAOBC的面积为的面积为4,4,反比例函数的图象反比例函数的图象的一支经过矩形对角线的交点的一支经过矩形对角线的交点P,P,则该反比例函数的解析式是则该反比例函数的解析式是(())A.B.C.D.A.B.C.D.xkyxy4xy21xy1xy2xPyOBAC典型例题知识点二利用图形的面积求解析式1.如图,点A是反...