6.3 实数第2课时.pptxVIP免费

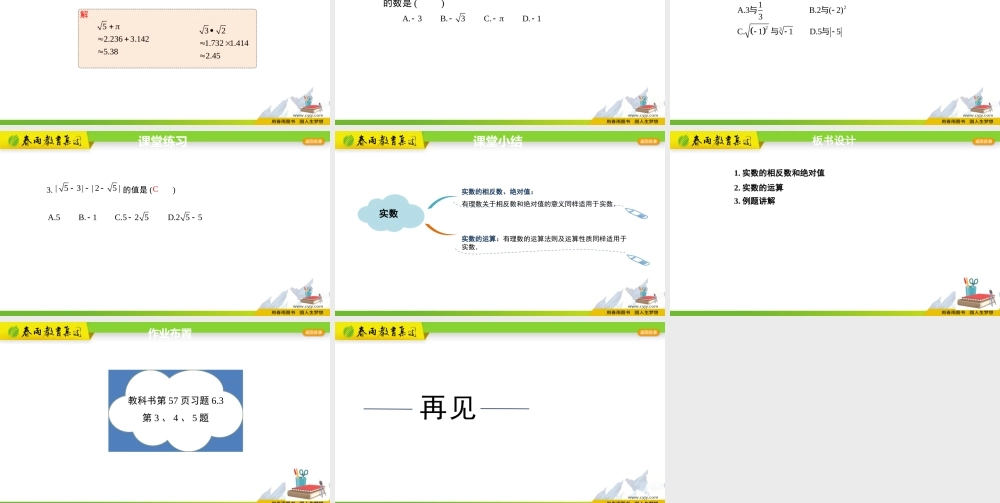
第六章实数6.3实数第2课时人教版同步课件学习目标1.了解实数的相反数和绝对值的意义。（重难点）2.认识实数范围内的运算法则，会进行实数的四则运算与近似计算。（重难点）3.在教学过程中通过渗透类比转化的思想，让学生意识到知识之间的紧密联系，体会数学的一致性。4.通过师生共同探索，体验独立思考与合作交流的学习过程，激发学生探索数学的热情和兴趣。只有符号不同的两个数,其中一个是另一个的相反数.什么是相反数？什么是绝对值？数轴上表示数a的点到原点的距离叫做数a的绝对值,用︱a︱表示.什么是倒数？如果两个数的积是1,则这两个数互为倒数.有理数中的几个重要概念:复习导入新知导入(1)的相反数是______，－π的相反数是______，0的相反数是______；22π0合作探究实数a的相反数为－a（a为任意实数）新知讲解(2)_______，|－π|=______，|0|=______.22π0合作探究正实数的绝对值是它本身；负实数的绝对值是它的相反数；0的绝对值是0.你能说说实数的绝对值的意义吗？aa>00a=0–aa<0实数=a新知讲解1.的相反数是________，绝对值是________.2.绝对值等于的数是________.33355有理数的相反数、绝对值等概念同样适用于实数，那么有理数的运算法则呢？小试牛刀新知讲解判断下列等式是否成立.若成立，这些等式用了什么运算律？3223322311323(2)3222333(23)353加法交换律乘法交换律乘法结合律加法结合律合作探究有理数的运算法则及运算性质同样适用于实数.新知讲解例1：(1)分别写出，的相反数；(2)指出，分别是什么数的相反数；解：(1)因为，所以的相反数分别为；(2)因为，所以分别是6π3.145313(6)6,(π3.14)3.14π33(5)5,(31)136,π3.146,3.14π35,1335,31典型例题新知讲解(3)求的绝对值；(4)已知一个数的绝对值是，求这个数.(3)因为，所以；(4)因为，所以绝对值为的数是或.3643336464433644433,3333典型例题新知讲解解例2计算下列各式的值：(1)(2)(32)23323(32)23(22)3033323(32)353典型例题新知讲解例3计算(结果保留小数点后两位)：(1)(2)532解52.2363.1425.38321.7321.4142.45典型例题新知讲解1.下列四个数：其中最小的数是()331、、、331A.B.C.D.C课堂练习2.下列各数中，互为相反数的是()2235A13)3.B.2(2C.D.115与与与与C课...