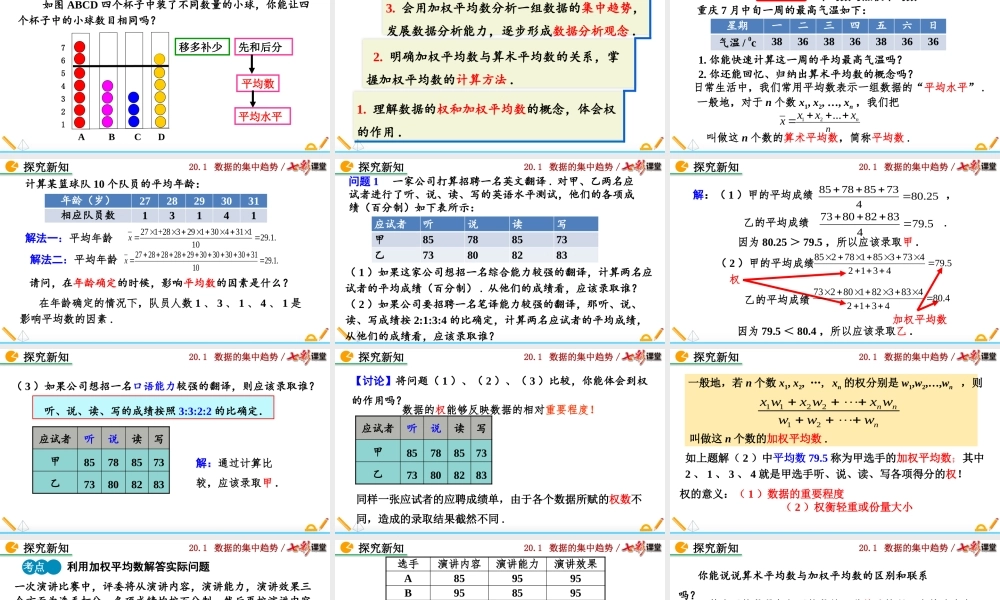
20.1数据的集中趋势/20.1数据的集中趋势20.1.1平均数(第1课时)人教版数学八年级下册20.1数据的集中趋势/7654321ABCD平均数先和后分移多补少如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?平均水平导入新知20.1数据的集中趋势/1.理解数据的权和加权平均数的概念,体会权的作用.2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.学习目标3.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.20.1数据的集中趋势/重庆7月中旬一周的最高气温如下:星期一二三四五六日气温/0c383638363836361.你能快速计算这一周的平均最高气温吗?2.你还能回忆、归纳出算术平均数的概念吗?日常生活中,我们常用平均数表示一组数据的“平均水平”.一般地,对于n个数x1,x2,…,xn,我们把12...nnxxxx叫做这n个数的算术平均数,简称平均数.探究新知知识点1平均数与加权平均数20.1数据的集中趋势/计算某篮球队10个队员的平均年龄:年龄(岁)2728293031相应队员数13141解法一:平均年龄解法二:平均年龄请问,在年龄确定的时候,影响平均数的因素是什么?在年龄确定的情况下,队员人数1、3、1、4、1是影响平均数的因素.271+28329130431129.1.10x2728282829303030303129.1.10x探究新知20.1数据的集中趋势/应试者听说读写甲85788573乙73808283(1)如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?(2)如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?问题1一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:探究新知20.1数据的集中趋势/解:(1)甲的平均成绩,25.80473857885乙的平均成绩.5.79483828073权加权平均数(2)甲的平均成绩5.794312473385178285乙的平均成绩4.804312483382180273探究新知因为79.5<80.4,所以应该录取乙.因为80.25>79.5,所以应该录取甲.20.1数据的集中趋势/(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?应试者听说读写甲85788573乙73808283听、说、读、写的成绩按照3:3:2:2的比确定.探究新知解:通过计算...