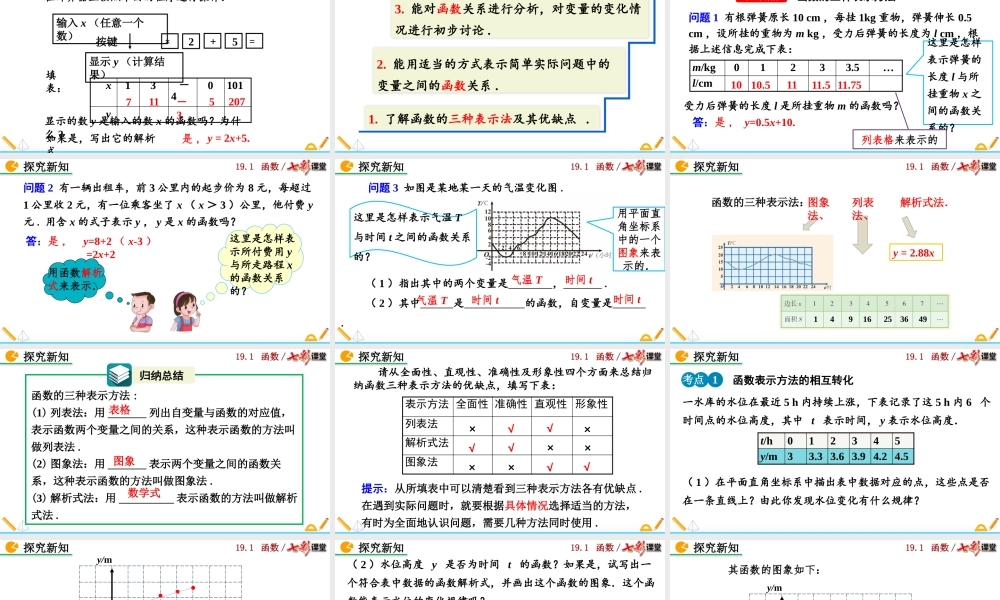
19.1函数/19.1函数19.1.2函数的图象(第2课时)人教版数学八年级下册19.1函数/在计算器上按照下面的程序进行操作:输入x(任意一个数)按键×=显示y(计算结果)x13-40101y711-35207显示的数y是输入的数x的函数吗?为什么?填表:+5如果是,写出它的解析式y=2x+5.导入新知2是,19.1函数/2.能用适当的方式表示简单实际问题中的变量之间的函数关系.1.了解函数的三种表示法及其优缺点.学习目标3.能对函数关系进行分析,对变量的变化情况进行初步讨论.19.1函数/问题1有根弹簧原长10cm,每挂1kg重物,弹簧伸长0.5cm,设所挂的重物为mkg,受力后弹簧的长度为lcm,根据上述信息完成下表:受力后弹簧的长度l是所挂重物m的函数吗?m/kg01233.5…l/cm答:是,y=0.5x+10.11.7511.51110.510这里是怎样表示弹簧的长度l与所挂重物x之间的函数关系的?列表格来表示的探究新知知识点函数的三种表示方法19.1函数/问题2有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了x(x>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?答:是,y=8+2(x-3)=2x+2探究新知这里是怎样表示所付费用y与所走路程x的函数关系的?用函数解析式来表示.19.1函数/问题3如图是某地某一天的气温变化图.(1)指出其中的两个变量是,.(2)其中是的函数,自变量是.气温T时间t气温T时间t时间t探究新知这里是怎样表示气温T与时间t之间的函数关系的?用平面直角坐标系中的一个图象来表示的.19.1函数/函数的三种表示法:y=2.88x图象法、列表法、解析式法.14916253649探究新知19.1函数/探究新知归纳总结函数的三种表示方法:(1)列表法:用_______列出自变量与函数的对应值,表示函数两个变量之间的关系,这种表示函数的方法叫做列表法.(2)图象法:用_______表示两个变量之间的函数关系,这种表示函数的方法叫做图象法.(3)解析式法:用__________表示函数的方法叫做解析式法.表格图象数学式19.1函数/请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表:表示方法全面性准确性直观性形象性列表法解析式法图象法提示:从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.√×××××√√√√√探究新知×19.1函数/一水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.(1)在平面直...