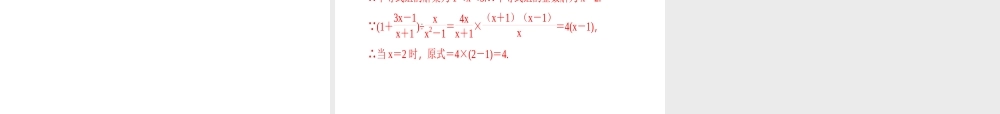专题二实数、整式、分式的运算与化简求值数学此类题目多以解答题的形式呈现,主要涉及的知识点有:绝对值、负整数指数幂、零次幂、-1的奇偶次幂、开方、平方、特殊角的三角函数值等,题目难度不大,但在每年的中考中必考.预计2018年中考继续考查的可能性很大.【例1】计算:(1)(2017·随州)(13)-2-(2017-π)0+(-3)2-|-2|.(2)(2017·孝感)-22+3-8+2·cos45°.解:原式=9-1+3-2=9.解:原式=-4-2+2×22=-4-2+1=-5.【例2】化简:(1)(2017·海南)(x+1)2+x(x-2)-(x+1)·(x-1).解:原式=x2+2x+1+x2-2x-x2+1=x2+2.(2)(2017·滨州)m3-n3m2+mn+n2÷m2-n2m2+2mn+n2.解:原式=(m-n)(m2+mn+n2)m2+mn+n2·(m+n)2(m+n)(m-n)=(m-n)·m+nm-n=m+n.【例3】先化简,再求值:(1)(2017·常州)(x+2)(x-2)-x(x-1),其中x=-2.解:原式=x2-4-x2+x=x-4,当x=-2时,x-4=(-2)-4=-6.(2)(导学号65244230)(2017·赤峰)(a-6a2-4-3a+2)÷aa-2,其中a=20170+(-15)-1+27·tan30°.解:原式=a-6(a+2)(a-2)×a-2a-3a+2×a-2a=a-6a(a+2)-3(a-2)a(a+2)=-2a+2, a=20170+(-15)-1+27tan30°,∴a=1-5+3=-1.∴原式=-2-1+2=-2.1.计算:(1)(2017·温州)2×(-3)+(-1)2+8;(2)(2017·黄石)(-2)3+16+10+|-3+3|;解:原式=-6+1+22=-5+22.解:原式=-8+4+1+3-3=-3.(3)(2017·陕西)(-2)×6+|3-2|-(12)-1;(4)(2017·深圳)|2-2|-2cos45°+(-1)-2+8;解:原式=-12+2-3-2=-23-3=-33.解:原式=2-2-2×22+1+22=2-2-2+1+22=3.(5)(2017·西宁)-22+(3-π)0+|1-2sin60°|;解:原式=-4+1+|1-2×32|=-3+3-1=3-4.(6)(2017·内江)-12017-|1-33tan60°|+(-2)2×(12)-2+(2017-π)0.解:原式=-1-|1-33×3|+2×4+1=-1-0+8+1=8.2.化简:(1)(2017·十堰)化简:(2a+1+a+2a2-1)÷aa-1;解:原式=2(a-1)+a+2(a+1)(a-1)·a-1a=2a-2+a+2a(a+1)=3aa(a+1)=3a+1.(2)(2017·乐山)(2a2+2aa2-1-a2-aa2-2a+1)÷2aa-1.解:原式=[2a(a+1)(a+1)(a-1)-a(a-1)(a-1)2]÷2aa-1=(2aa-1-aa-1)÷2aa-1=aa-1÷2aa-1=aa-1·a-12a=12.3.先化简,再求值:(1)(2017·恩施州)x-2x2+2x÷x2-4x+4x2-4-12x,其...