高二数学人教A版选修2-1课件：3.1.3 空间向量的数量积运算 .pptVIP免费

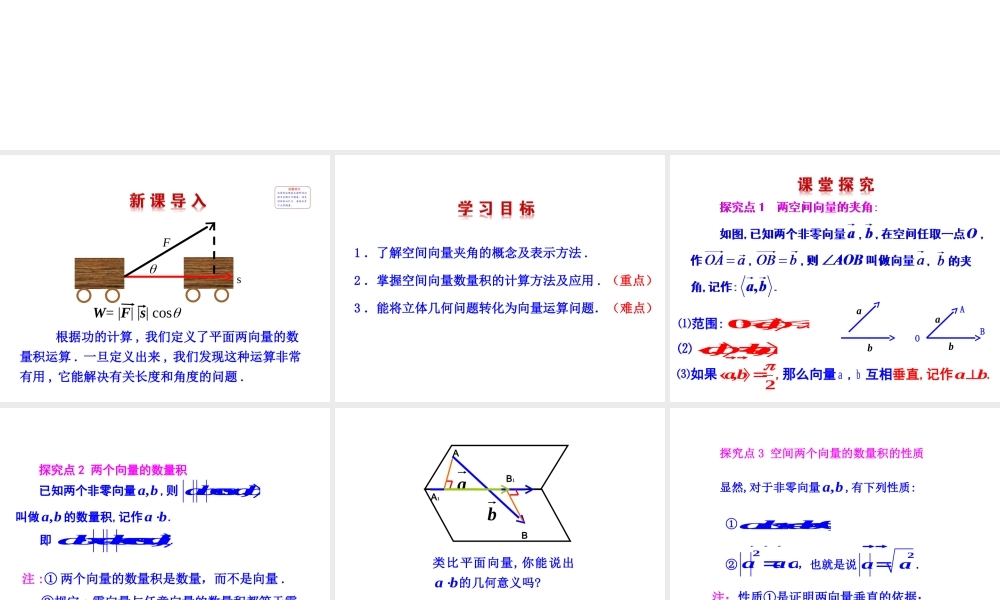
3.1.3空间向量的数量积运算sF�W=|F||s|cos根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度的问题.1．了解空间向量夹角的概念及表示方法.2．掌握空间向量数量积的计算方法及应用.（重点）3．能将立体几何问题转化为向量运算问题．（难点）OABaabb⑴范围:0,.≤≤ab⑶如果,2ab,那么向量a,b互相垂直,记作ab.⑵,,.abba＝注:①两个向量的数量积是数量，而不是向量.②规定:零向量与任意向量的数量积都等于零.探究点2两个向量的数量积已知两个非零向量,ab,则cos,abab叫做,ab的数量积,记作ab.即cos,ababab.abA1B1BA类比平面向量,你能说出ab的几何意义吗?如图11AB�是b在a方向上的射影向量.探究点3空间两个向量的数量积的性质显然,对于非零向量,ab,有下列性质:①0;abab②2aaa，也就是说2aa.注：性质①是证明两向量垂直的依据；性质②是求向量的长度（模）的依据.注：性质①是证明两向量垂直的依据；性质②是求向量的长度（模）的依据.探究点4空间向量的数量积满足的运算律⑴()()abab.⑵abba(交换律).⑶()abcabac(分配律).注：向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立.注：向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立.例1在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.已知:如图,,POPA分别是平面的垂线、斜线，AO是PA在平面内的射影，l，且lOA.求证：lPA.PAl分析：用向量来证明两直线垂直，只需证明两直线的方向向量的数量积为零即可！线证证为����������在直l上取向量a,只要a×PA=0因a×PO=0,a×OA=0所以a×PA=a×(PO+OA)=a×PO+a×OA=明0所以a⊥PA,即：l⊥PA.POAla逆命题成立吗?在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.分析：要证明一条直线与一个平面垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.,,,,:2.线内两条线证已知直是平面的相交直果例如求mnlmlnllmngng�m�l取已知平面内的任一条直...