高中数学（人教版A版必修一）配套课件：第一章 集合与函数的概念 习题课.pptxVIP免费

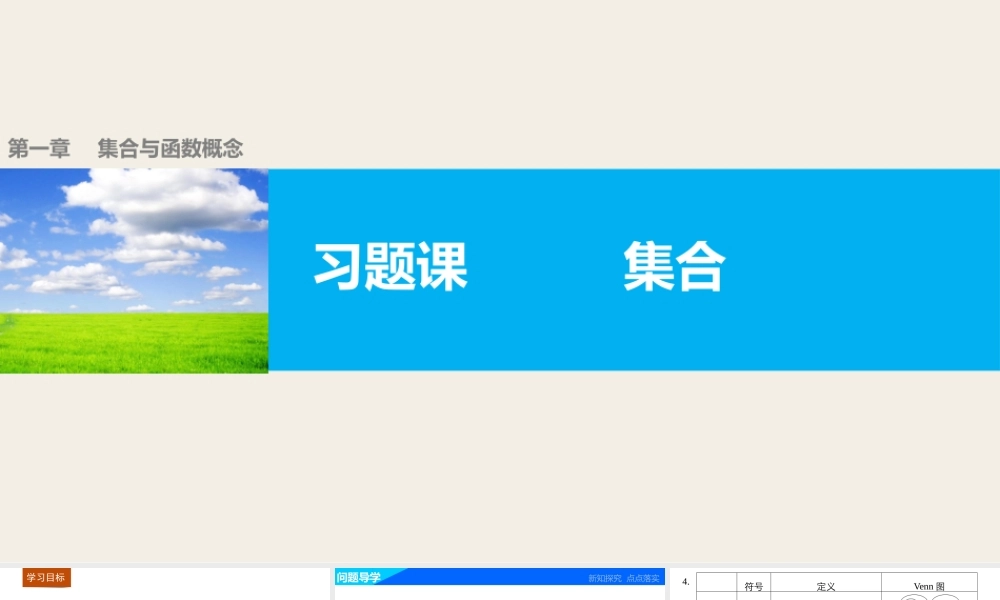
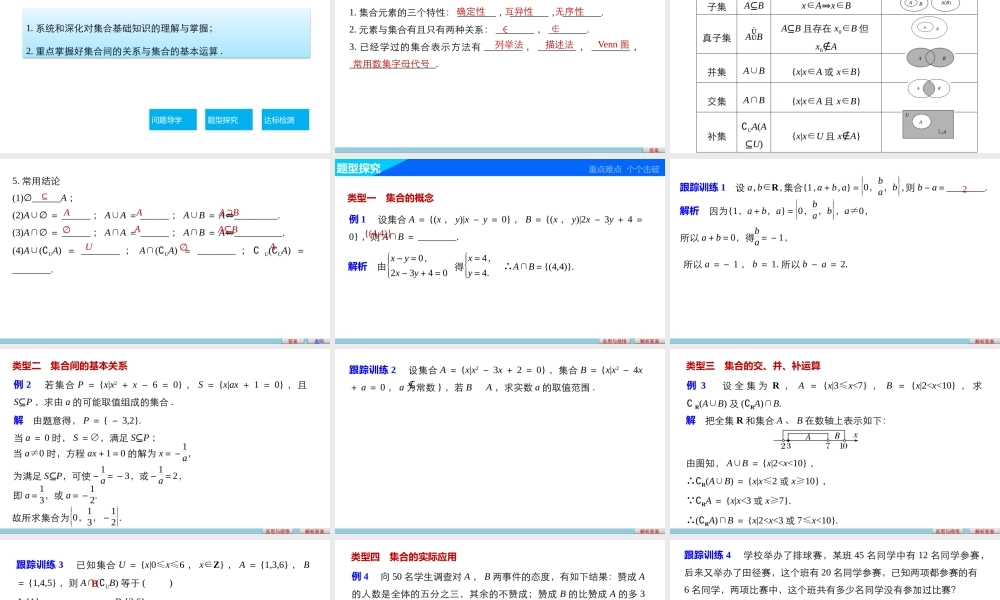
习题课集合第一章集合与函数概念1.系统和深化对集合基础知识的理解与掌握；2.重点掌握好集合间的关系与集合的基本运算.问题导学题型探究达标检测学习目标问题导学新知探究点点落实1.集合元素的三个特性：________，________，________.2.元素与集合有且只有两种关系：________，________.3.已经学过的集合表示方法有________，________，________，__________________.答案确定性互异性无序性∈∉列举法描述法Venn图常用数集字母代号4.符号定义Venn图子集A⊆Bx∈A⇒x∈B真子集ABA⊆B且存在x0∈B但x0∉A并集A∪B{x|x∈A或x∈B}交集A∩B{x|x∈A且x∈B}补集∁UA(A⊆U){x|x∈U且x∉A}5.常用结论(1)∅______A；(2)A∪∅＝______；A∪A＝______；A∪B＝A⇔_________.(3)A∩∅＝______；A∩A＝______；A∩B＝A⇔__________.(4)A∪(∁UA)＝________；A∩(∁UA)＝________；∁U(∁UA)＝________.答案⊆AAA⊇B∅AA⊆BU∅A返回题型探究重点难点个个击破类型一集合的概念例1设集合A＝{(x，y)|x－y＝0}，B＝{(x，y)|2x－3y＋4＝0}，则A∩B＝________.解析由x－y＝0，2x－3y＋4＝0得x＝4，y＝4.∴A∩B＝{(4,4)}.解析答案{(4,4)}反思与感悟解析答案所以a＝－1，b＝1.所以b－a＝2.跟踪训练1设a，b∈R，集合{1，a＋b，a}＝0，ba，b，则b－a＝________.解析因为{1，a＋b，a}＝0，ba，b，a≠0，所以a＋b＝0，得ba＝－1，2类型二集合间的基本关系例2若集合P＝{x|x2＋x－6＝0}，S＝{x|ax＋1＝0}，且S⊆P，求由a的可能取值组成的集合.当a≠0时，方程ax＋1＝0的解为x＝－1a，解析答案解由题意得，P＝{－3,2}.当a＝0时，S＝∅，满足S⊆P；为满足S⊆P，可使－1a＝－3，或－1a＝2，即a＝13，或a＝－12.故所求集合为0，13，－12.反思与感悟解析答案跟踪训练2设集合A＝{x|x2－3x＋2＝0}，集合B＝{x|x2－4x＋a＝0，a为常数}，若BA，求实数a的取值范围.⊈类型三集合的交、并、补运算例3设全集为R，A＝{x|3≤x<7}，B＝{x|2