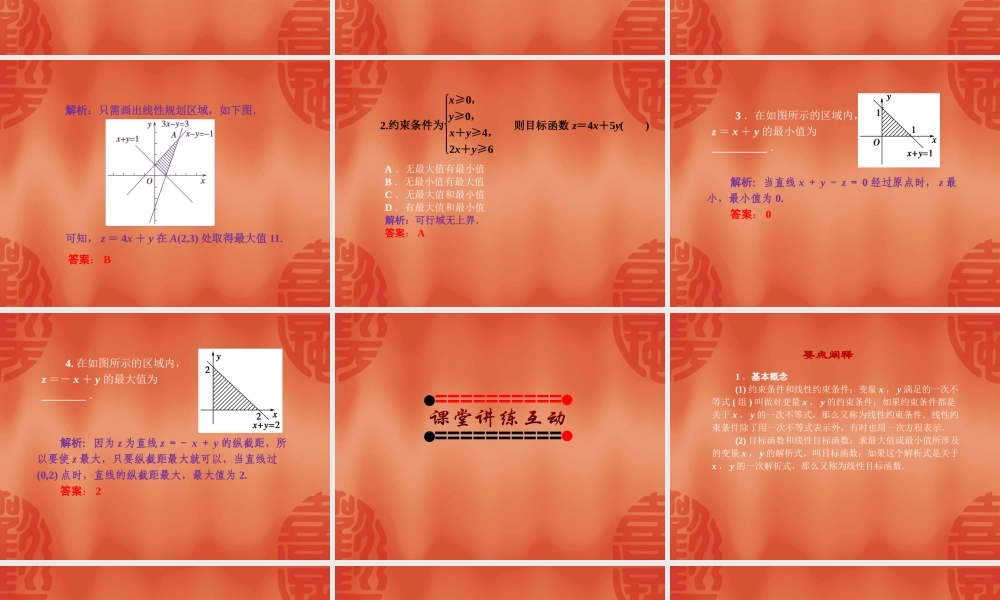
3.3.2简单的线性规划问题了解线性规划的意义,了解线性规划的基本概念,掌握线性规划问题的图解法,并能应用线性规划的方法解决一些简单的实际问题,提高解决实际问题的能力.1.关于x,y的不等式(组)称为对变量x,y的约束条件,如果约束条件都是关于x,y的一次不等式,则称约束条件为________约束条件.答案:线性2.把要求最大(小)值的函数z=f(x,y)称为________函数.答案:目标自学导引3.在线性约束条件下求线性目标函数的最大值或最小值问题,称为________规划问题.满足线性约束条件的解(x,y)叫做________解,由所有可行解组成的集合叫做________域,其中,使目标函数取得最大值或最小值的可行解叫做最优解.答案:线性可行可行线性目标函数z=2x+3y最大值的几何意义是什么?自主探究答案:由y=-23x+z3知,直线经过平面区域的截距最大时,目标函数有最大值.A.4B.11C.12D.14预习测评1.设变量x,y满足约束条件x-y≥-1,x+y≥1,3x-y≤3.则目标函数z=4x+y的最大值为()解析:只需画出线性规划区域,如下图.可知,z=4x+y在A(2,3)处取得最大值11.答案:BA.无最大值有最小值B.无最小值有最大值C.无最大值和最小值D.有最大值和最小值解析:可行域无上界.答案:A2.约束条件为x≥0,y≥0,x+y≥4,2x+y≥6则目标函数z=4x+5y()3.在如图所示的区域内,z=x+y的最小值为__________.解析:当直线x+y-z=0经过原点时,z最小,最小值为0.答案:04.在如图所示的区域内,z=-x+y的最大值为________.解析:因为z为直线z=-x+y的纵截距,所以要使z最大,只要纵截距最大就可以,当直线过(0,2)点时,直线的纵截距最大,最大值为2.答案:21.基本概念(1)约束条件和线性约束条件:变量x,y满足的一次不等式(组)叫做对变量x,y的约束条件;如果约束条件都是关于x,y的一次不等式,那么又称为线性约束条件.线性约束条件除了用一次不等式表示外,有时也用一次方程表示.(2)目标函数和线性目标函数:求最大值或最小值所涉及的变量x,y的解析式,叫目标函数;如果这个解析式是关于x,y的一次解析式,那么又称为线性目标函数.要点阐释(3)线性规划问题:一般地,在线性约束条件下,求线性目标函数的最大值或最小值问题,统称为线性规划问题.(4)可行解与可行域:满足线性约束条件的解(x,y)叫做可行解.由所有可行解组成的集合叫做可行域.(5)最优解:使目标函数取得最大值或最小值的可行解,称为这个问...