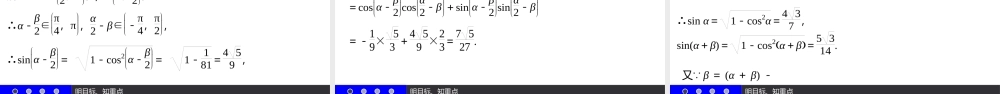第三章三角恒等变换§3.1两角和与差的正弦、余弦和正切公式3.1.1两角差的余弦公式明目标、知重点明目标知重点填要点记疑点探要点究所然内容索引010203当堂测查疑缺04明目标、知重点1.了解两角差的余弦公式的推导过程.2.理解用向量法导出公式的主要步骤.3.熟记两角差的余弦公式的形式及符号特征,并能利用该公式进行求值、计算.明目标、知重点明目标、知重点两角差的余弦公式C(α-β):cos(α-β)=,其中α、β为任意角.cosαcosβ+sinαsinβ填要点·记疑点明目标、知重点探要点·究所然情境导学明目标、知重点探究点一两角差余弦公式的探索思考1有人认为cos(α-β)=cosα-cosβ,你认为正确吗,试举两例加以说明.答不正确.例如:当α=π2,β=π4时,cos(α-β)=cosπ4=22,而cosα-cosβ=cosπ2-cosπ4=-22,明目标、知重点cos(α-β)≠cosα-cosβ;再如:当α=π3,β=π6时,cos(α-β)=cosπ6=32,而cosα-cosβ=cosπ3-cosπ6=1-32,cos(α-β)≠cosα-cosβ.明目标、知重点思考2请你计算下列式子的值,并根据这些式子的共同特征,写出一个猜想.①cos45°cos45°+sin45°sin45°==;②cos60°cos30°+sin60°sin30°==;③cos30°cos120°+sin30°sin120°==;④cos150°cos210°+sin150°sin210°==.猜想:cosαcosβ+sinαsinβ=;即:.1cos0°32cos30°0cos(-90°)12cos(-60°)cos(α-β)cos(α-β)=cosαcosβ+sinαsinβ明目标、知重点探究点二两角差余弦公式的证明如图,以坐标原点为中心,作单位圆,以Ox为始边作角α与β,设它们的终边分别与单位圆相交于点P,Q,请回答下列问题:(1)P点坐标是,向量OP→=,|OP→|=.Q点坐标是,向量OQ→=,|OQ→|=.(cosα,sinα)(cosα,sinα)1(cosβ,sinβ)(cosβ,sinβ)1明目标、知重点(2)当α为钝角,β为锐角时,α-β和向量OP→与OQ→的夹角〈OP→,OQ→〉之间的关系是:;当α为锐角,β为钝角时,α-β和向量OP→与OQ→的夹角〈OP→,OQ→〉之间的关系是:;当α,β均为任意角时,α-β和〈OP→,OQ→〉的关系是:.α-β=〈OP→,OQ→〉α-β=-〈OP→,OQ→〉α-β=2kπ±〈OP→,OQ→〉,k∈Z明目标、知重点(3)向量OP→与OQ→的数量积OP→·OQ→=|OP→||OQ→|·cos〈OP→,OQ→〉=;另一方面,OP→与OQ→的数量积用点坐标形式表示:OP→·OQ→=(cosα,sinα)·(cosβ,sinβ)=.从而,对任意角α,β均有c...