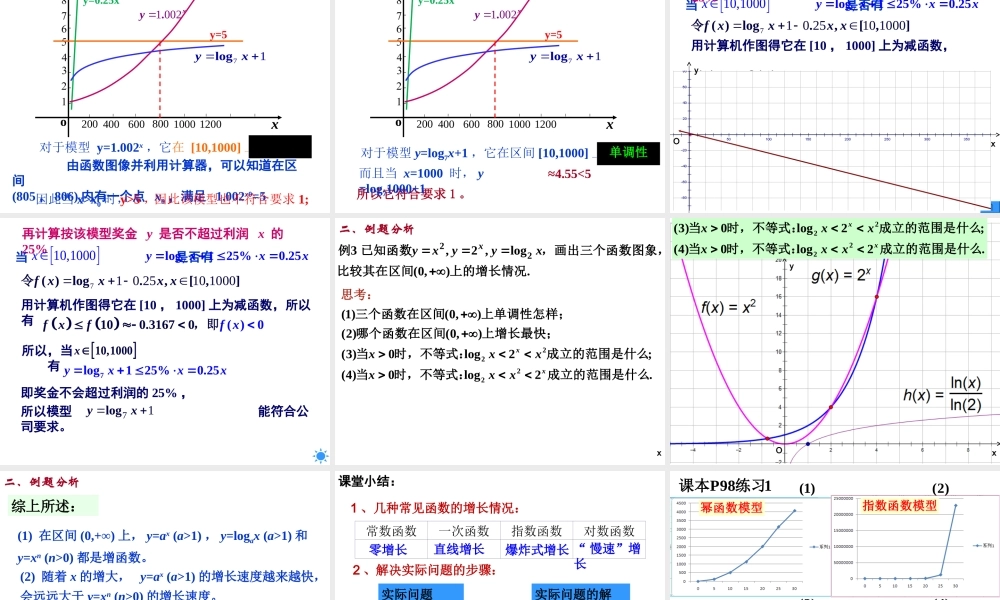
3.2.1几类不同增长的函数模型一、新课引入有人说,一张普通的纸对折30次之后高度会超过10座珠穆朗玛峰,你相信吗?解:设纸厚度为0.01cm,一张纸对折x次的厚度是0012().xfxcm30300012().()fcm751071010710..cmm约8844米实例2根据历史传说记载,国际象棋起源于古印度,至今见诸于文献最早的记录是在萨珊王朝时期用波斯文写的.据说,有位印度教宗师见国王自负虚浮,决定给他一个教训。他向国王推荐了一种在当时尚无人知晓的游戏。国王对这种新奇的游戏很快就产生了浓厚的兴趣,便问宗师想要得到什么赏赐。宗师开口说道:请您在棋盘上的第一个格子上放1粒麦子,第二个格子上放2粒,第三个格子上放4粒,第四个格子上放8粒……即每一个次序在后的格子中放的麦粒都必须是前一个格子麦粒数目的2倍,直到最后一个格子第64格放满为止,这样我就十分满足了。你知道这需要多少麦粒吗?26364191222211910.()粒100040g按颗麦粒约计算,19191000470001000..()亿吨66.全球年小麦产量约亿吨例1、假设你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。请问,你会选择哪种投资方案?二、例题分析解:设第x天所得回报是y元方案一可以用函数进行描述;y=40(xN*)∈方案二可以用函数进行描述;y=10x(xN*)∈方案三可以用函数进行描述.y=0.4×2x-1(xN*)∈我们来计算三种方案所得回报的增长情况:第x/天方案一方案二方案三y/元y/元y/元增加量增加量增加量1234040400010203010100.40.81.60.40.8045678…30………………4040404040400000040506070803001010101010103.26.412.825.651.2214748364.81.63.26.412.825.6107374182.4y=40y=10xy=0.4×2x-1从表格中获取信息,体会三种函数的增长差异。2亿1亿下面利用图象从整体上把握不同函数模型的增长:1234678911二、例题分析我们看到,底为2的指数函数模型比一次函数模型增长速度要快得多。1234678911二、例题分析下面利用图象从整体上把握不同函数模型的增长:根据以上的分析,是否应作这样的选择:投资5天以下选方案一,投资5~8天选方案二,投资8天以上选方案三?8结论:投资1~6天,应选择方案一;投资7天,可选择方案一或方案二;投资8~10天,应选择方案二;投资11天以上(含11天),应选择方案三。总天数回报...