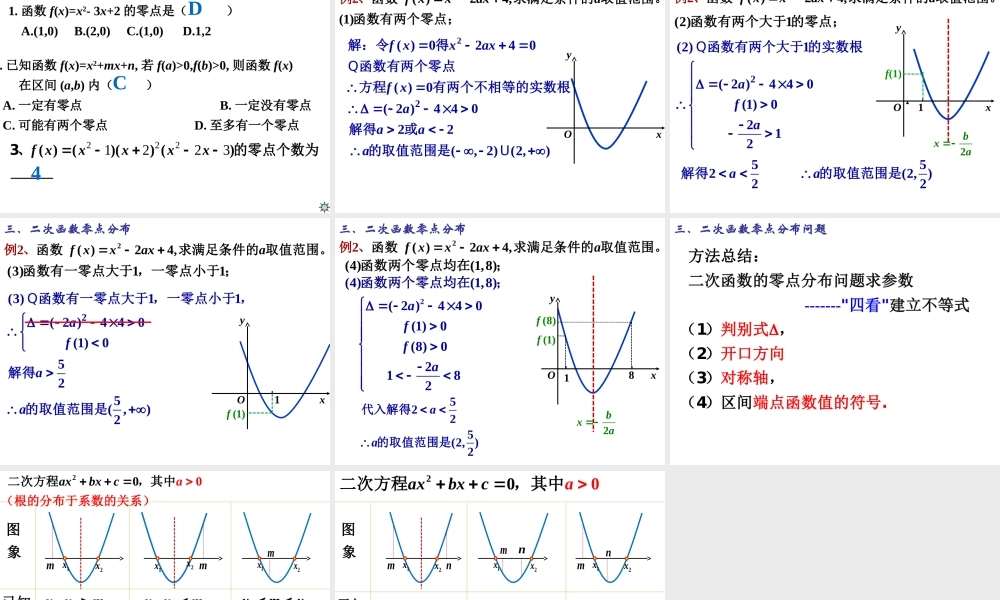
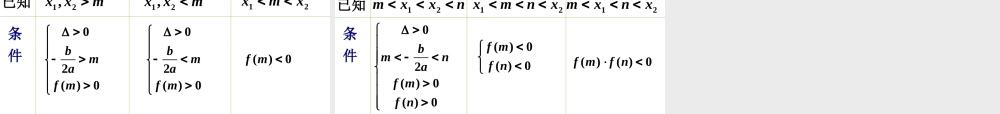3.1.1方程的根与函数的零点(第2课时)2:4(3,1)(30,,3),1xxxx解由题意可得:解是得或定义域24()log(43).fxxx作业:判断函数的单调性2243(2)7(,1)(3,)0,txxxxtU令,当时24()log(43)(,1)(3,).fxxx函数在区间上单调递减,在区间上单调递增4lo()g,0,tyt,22(,1),43(0,)(3),43(0,)xtxxtxtxxt当时单调递减,此时;当,时单调递增,此时;2(0,+)logtyt而当时,单调递增,①求定义域④”同增异减”下结论②确定内外函数,求中间量范围③分析内外函数单调性3、零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c(∈a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。思考1:如果函数y=f(x)在区间[a,b]上是一条连续不断的曲线,且在区间(a,b)内有零点,是否一定有f(a)·f(b)<0?三、基础知识讲解2232,4(-2,4)(2)(4)______0.yxxff在区间上连续,且在上__________零点,而xy-1O1234存在不一定3、零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c(∈a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。三、基础知识讲解思考2:如果函数y=f(x)在区间[a,b]上是一条连续不断的曲线,且有f(a)·f(b)>0,是否可以判断函数y=f(x)在(a,b)内没有零点?2232,4(2)(4)______0(-2,4)yxxff在区间上连续,且在上函数_______零点,存在xy-1O1234不可以3、零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c(∈a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。三、基础知识讲解1、图象是连续不断的曲线2()()0fafb、零点存在X注2:该定理只能解决存在零点,不一定唯一若需要证明有唯一零点,还需要确保函数为单调函数。23()712.fxxx例、已知,求该函数的零点个数2()0712(3)(4)0fxxxxx解:令得即(1)直接法利用对应的判断(求)函数零点(个方程的不相等的实数数):根的个数271203,4xx两个不相等的实数根方程有:;3,4.函数有,分别是两个零点22(7)412107120xx方两个不相等的法2:...