高一数学人教A版必修1课件：2.3 幂函数 .pptVIP免费

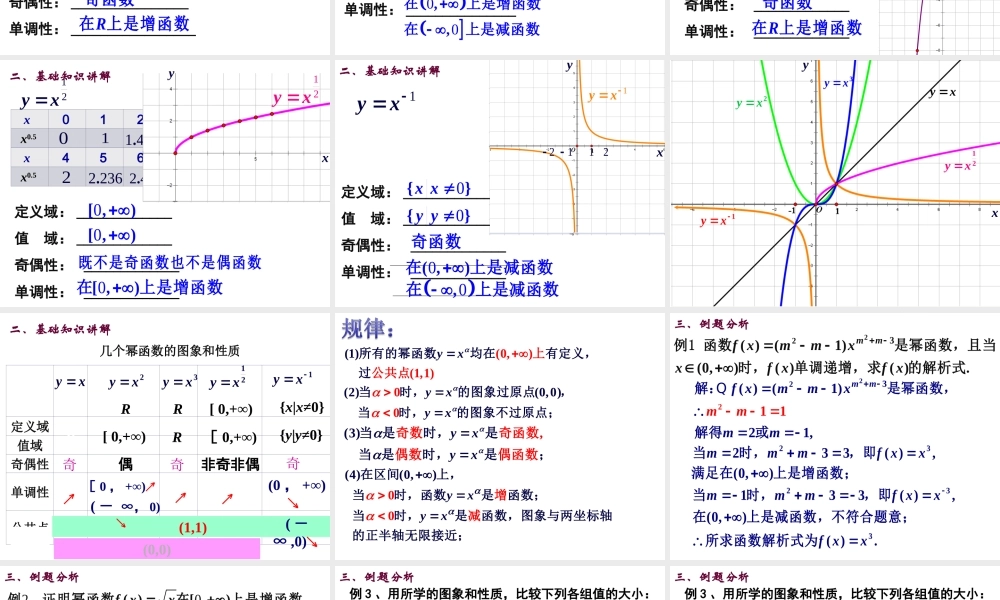
2.3幂函数一、实例探究1、如果小红购买了每千克1元的水果x千克，那么她需要付的钱数y是2、如果正方形的边长为x，那么正方形的面积y为3、如果正方体的边长为x，那么正方体的体积y为4、如果正方形场地面积为x，那么正方形的边长y为5、如果小兰在x秒内骑车行进了1km，那么她骑车的速度y是yx2yx3yx12yx1yx1、幂函数的定义：一般的，函数y=xα叫做幂函数，其中x是自变量，α是常数。15011022334561().;();();();();()xxyyyxxyxyxy下列哪些是幂函数？(2)(5)二、基础知识讲解关于幂函数，主要学习下列几种函数的图象与性质.1()yx22()yx33()yx124()yx15()yx二、基础知识讲解值域：____________奇偶性：________________单调性：_________________R奇函数R在上是增函数yxROyxyx二、基础知识讲解定义域：____________2yx值域：_____________奇偶性：______________单调性：_______________R0,偶函数00,,在上是增函数在上是减函数2yx二、基础知识讲解定义域：_____________Oyxx-2-1.5-1-0.50x3x0.511.52x383375.1083375.1定义域：_____________值域：_____________奇偶性：_____________单调性：_____________R奇函数R在上是增函数R3yx二、基础知识讲解0125.0125.3yxOxyx0123x0.5x456x0.5011414.1732.245.2236.2定义域：_____________值域：_____________奇偶性：_____________单调性：_____________0[,)在上是增函数0[,)既不是奇函数也不是偶函数0[,)12yx二、基础知识讲解12yxyx定义域：_____________值域：_____________奇偶性：_____________单调性：_____________0{}xx奇函数0(,)在上是减函数0,在上是减函数0{}yy1yx1yx2112二、基础知识讲解yx2yxyx3yx1yx12yxyx定义域值域奇偶性单调性公共点奇偶奇非奇非偶奇(1,1)(0,0)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)［0,+∞)［0，+∞)↗(－∞，0)↘↗↗↗几个幂函数的图象和性质yx2yx3yx12yx1yx(0，+∞)↘(－∞,0)↘二、基础知识讲解(0,)()1,1)(1yx所有的幂函数均在有定义，公共点过上(2)(0,000)yxyx当时，的图象过原点，当时，的图象不过原点；(3),yxyx当是时，是奇数奇当是时，是；函数偶数偶函数(4)()000,yxyx在区间上，当时，函数是函数；当时，是函数，图象与两坐标轴的正半增减轴无限接近...