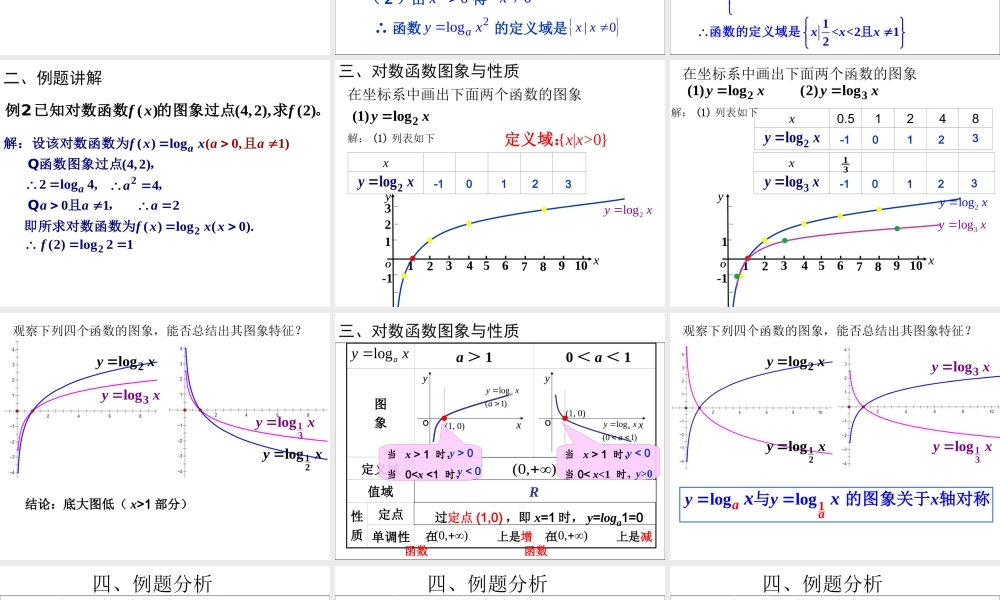
高一数学人教A版必修1课件：2.2.2 对数函数及其性质（第1课时） .pptVIP免费

下载本文档

阅读 0
下载 0
格式 ppt
大小 1.21 MB
约23页
2024-02-16
收藏
评论
点赞(0)
海报
举报

在线预览已结束，请下载后查看完整版，加入VIP享文档下载特权

/23

文本预览下载提示常见问题

2.2.2对数函数及其性质（第1课时）课前复习：1、指数式与对数式的互化xaNlogaxN01a图象性质1a定义域值域1xOy1xOyRxya(0,+)(0,1)过定点恒001=xya即时，恒有R在上是增函数001xy当时，01>>xy当时，R在上是减函数01>xy当时，01><0(3)21148>0xxx由题意可得1>211,<<212<2xxxxx解得即且1<<212xxx函数的定义域是且()(4,2),(2)fxf例2已知对数函数的图象过点求。()log(0,1)aafxxa解：设该对数函数为且(4,2)2log4,a函数图象过点，Q24a，2()log(0).fxxx即所求对数函数为012aaa且，Q2(2)log21f二、例题讲解三、对数函数图象与性质在坐标系中画出下面两个函数的图象2(1)logyx解：(1)列表如下{|>0}xx定义域：x0.51248-101232logyx-11345678910xyO122logyx23在坐标系中画出下面两个函数的图象2(1)logyx解：(1)列表如下3(2)logyx-11345678910xyO122logyxx13927-101233logyx133logyxx0.51248-101232logyx2logyx3logyx12logyx13logyx观察下列四个函数的图象，能否总结出其图象特征？结论：底大图低（x>1部分）三、对数函数图象与性质图象定义域值域性质定点单调性a＞10＜a＜1oyx(1,0))1(logaxyaoyx(1,0))10(logaxya),0(R过定点(1,0)，即x=1时，y=loga1=0在上是增函数),0(在上是减函数),0(当x>1时，当00y<0当x>1时，当00logayx2logyx3log...

1、当您付费下载文档后，您只拥有了使用权限，并不意味着购买了版权，文档只能用于自身使用，不得用于其他商业用途（如 [转卖]进行直接盈利或[编辑后售卖]进行间接盈利）。
2、本站所有内容均由合作方或网友上传，本站不对文档的完整性、权威性及其观点立场正确性做任何保证或承诺！文档内容仅供研究参考，付费前请自行鉴别。
3、如文档内容存在违规，或者侵犯商业秘密、侵犯著作权等，请点击“违规举报”。

碎片内容