高一数学人教A版必修1课件：2.1.2 指数函数及其性质（1） .pptVIP免费

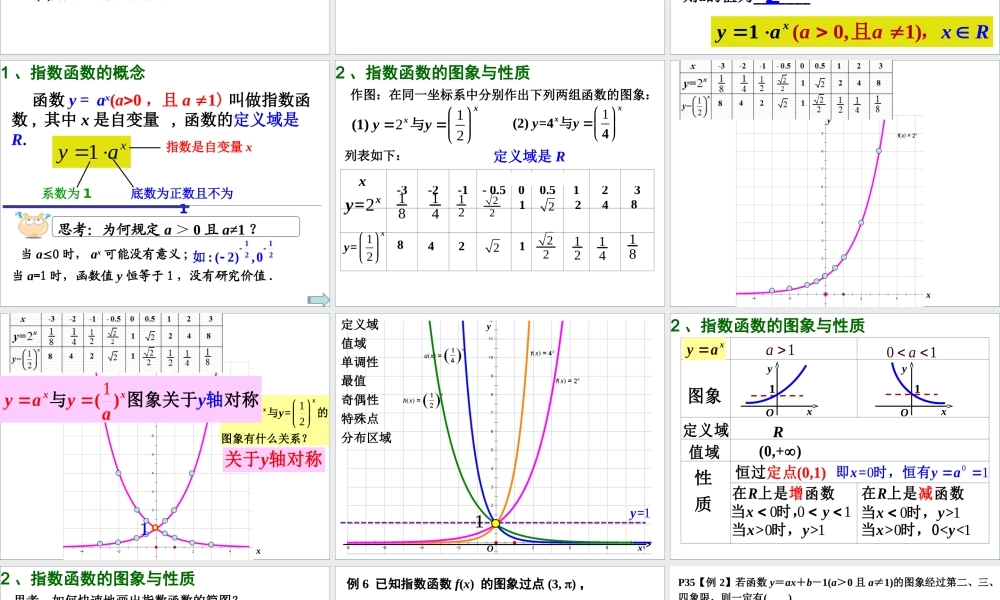
2.1.2指数函数及其性质（1）某种细胞分裂时，按照一分为二的规律，可由1个分裂成2个，2个分裂成4个，4个分裂成8个，8个分裂成16个，……如此下去，一个这样的细胞第x次分裂后，细胞的个数y是多少？2xy情景引入1截取次数木棰剩余长度1次2次3次4次x次尺21尺41尺81尺1611()2x尺12()xy情景引入2……壹尺之棰日取其半萬世不竭！庄子云：情景引入3据调查，现行银行存款定期一年利率是1.75%，某投资者打算存款1万元，按照复利计算，设x年(x≤20)底存款数为y万元,求函数关系式.117510175(.%).xxy1();均为幂的形式2();底数是一个正的常数3().x自变量都在指数位置xy)21(xy2思考思考::以上三个函数形式上有何共同特征?xya1.0175xy形如y=ax(a0，且a1)的函数叫做指数函数,其中x是自变量,函数的定义域是R.1、指数函数的概念xay1系数为1底数为正数且不为1指数是自变量x1、下列函数中，哪些是指数函数?练习(0,1)1xyaxRaa且，101221013210456710109()()()()()()()()(,)xxxxxxyyyyxyyxyaaa且2332()xyaaaa、已知函数是指数函数，则的值为_______√√√2函数y=ax(a0，且a1)叫做指数函数,其中x是自变量,函数的定义域是R.当a0时，ax可能没有意义;当a=1时，函数值y恒等于1，没有研究价值.1、指数函数的概念思考：为何规定a＞0且a≠1？1122:(2),0如xay1系数为1底数为正数且不为1指数是自变量xx-3-2-1-0.500.5123作图：在同一坐标系中分别作出下列两组函数的图象：122(1)xxyy与1(2)=44xxyy与列表如下：2=xy12=xy2、指数函数的图象与性质定义域是R18141222122488422122121418xyxy122==xxyy函数与的图象有什么关系？y关于轴对称11()xxyyaya与图象关于轴对称yx1=yO1定义域值域单调性最值奇偶性特殊点分布区域2、指数函数的图象与性质01a图象性质1a定义域值域Rxya(0,+)(0,1)过定点恒001=xya即时，恒有R在上是增函数001xy当时，01>>xy当时，R在上是减函数01>xy当时，01><