高一数学人教A版必修1课件：1.3.2 奇偶性（第2课时）.pptVIP免费

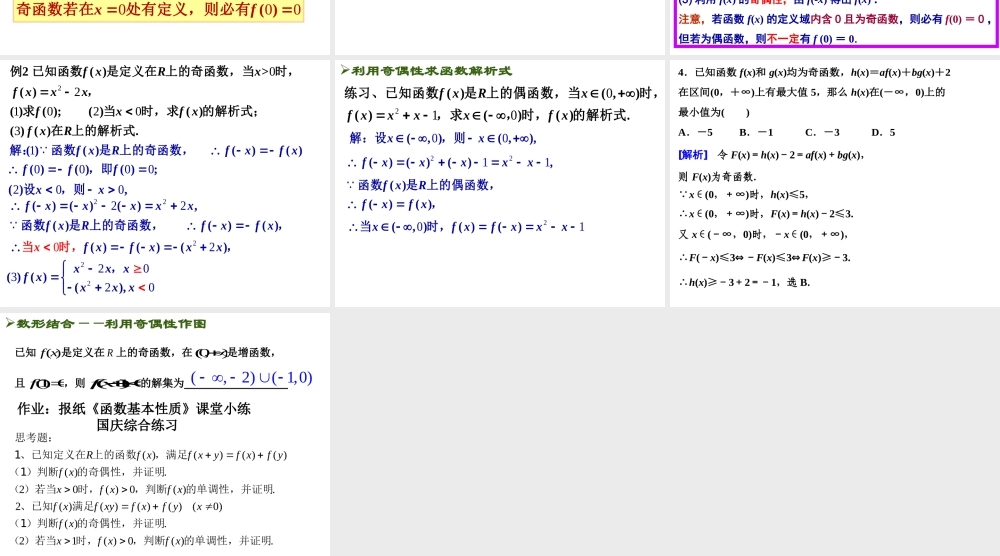
1.3.2奇偶性（第2课时)()()()()()(),()()()()fxgxhxfxgxfxgxpxfxgx1、已知为奇函数，为偶函数，证明为奇函数；2、已知均为偶函数，证明为偶函数偶函数在对称区间上的单调性______,取值范围______;奇函数在对称区间上的单调性______,取值范围_______;相反相同相同相反奇函数、偶函数的定义域必关于原点对称()(0,)(,0)fx1、已知为奇函数，在存在最大值3，则在上存在最（）值为（）222220()[,],()[[0,2]()[]]fffxxx解：是定义在上的奇函数，且在上单调递增在，上单调递增，即在，上单调递增，1()(),fmfm121()()();()()()().fxRxfxxxfxfxfxR例已知函数是定义在上的奇函数，当时，，求当时，求的解析式；在上的解析式10000()()()()()()();fxRfxfxfff解：函数是上的奇函数，，即利用奇偶性求函数解析式202202()>()()()fxRxfxxxxfx例已知函数是定义在上的奇函数，当时，，当时，求的解析式；200(),xx，则设()()()fxRfxfx函数是上的奇函数，，202()(),()xfxfxxx当时，2222()()(),fxxxxx[一点通]利用奇偶性求解析式(1)“求谁设谁”，求哪个区间的解析式，就把x设在哪个区间．(2)通过f(-x)，利用已知区间的解析式进行代入．(3)利...